
Peter Sørensen:
Matematik C
interaktivt for hf
(Blåt
hæfte)
Version 6.5
DEL 2
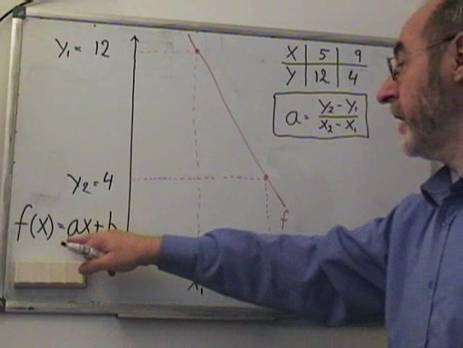

© PeterSoerensen.dk
©
PeterSoerensen.dk :
Kan
frit printes og fotokopiers af institutioner,
der har aftale med CopyDan
Matematik C
interaktivt for hf
(Blåt
hæfte)
Version 6.5
DEL 2
Forord.. 4
Lektion 15:
Potens-funktioner.. 5
Sådan findes en
regneforskrift 6
Sammenhæng mellem x og
y ved potens-vækst 6
Tegning af graf for en
potens-funktion. 8
Lektion 16:
Statistik.. 9
Ikke
grupperede observationer.. 9
Boksplot (eller
kassediagram): 10
Definition af
middeltal ved ikke grupperede observationer. 10
Grupperede
observationer.. 10
Boksplot
kan bruges både ved.. 11
Histogram.. 11
Middeltal ved grupperede
observationer. 11
Sumkurve. 12
Kumuleret hyppighed. 12
Kumuleret frekvens. 12
Definition af
median og kvartiler.. 13
Ved ikke grupperede
observationer defineres således: 13
Ved grupperede
observationer defineres således: 13
Lektion 17: Repetition
og flere beviser mv. 14
Geometri 14
Vinkelsummen i en
trekant er 180°. 15
Vinkelsummen af de to
spidse vinkler i en retvinklet trekant er 90°. 15
Pythagoras’s sætning. 15
Definition af Sinus og
Cosinus. 18
Bevis for Sinus- og
Cosinusformlerne. 20
Tangens. 21
Lineær
funktion.. 21
Potensfunktioner.. 24
Lektion 18 Mundtlig
eksamen.. 26
Eksempel på
undervisningsbeskrivelse. 26
Eksempel på
eksamens-spørgsmål. 26
Om Eksamen.. 28
Eksempler på
dispositioner.. 29
1. Procent- og
rentesregning. 29
2. Procent- og
rentesregning. 29
3. Variabelsammenhænge
og grafer. 30
4. Variabelsammenhænge
og grafer. 30
5. Lineær vækst 30
6. Lineær vækst 30
7. Eksponentiel vækst 30
8. Eksponentiel vækst 31
9. Eksponentiel vækst 31
10. Potensfunktioner. 31
12. Trekantsberegning. 32
13. Trekantsberegning. 32
14. Trekantsberegning. 32
16. Statistik. 34
2) Se
Videoer med demo af mundtlig eksamen Variabelsammenhænge (De første 2
min er i forringet billedkvalitet) 34
Procent og
rentesregning. 34
Trekantberegning
(samme video som i Lektion 17) 34
Lineær Vækst 34
Eksponentiel vækst 34
Potensfunktioner. 34
Statistik. 34
Facitliste for
vejledende eksamensopgaver.. 35
Facitliste for
”Vejledende prøvesæt 1” Fra og med opg. 2001 i opgavehæftet.. 41
Facitliste til
”vejledende prøvesæt 2” Fra og med opgave 2010 i opgavehæftet.. 43
Formelsamling Mat. C.. 46
Brøker.. 46
Parenteser.. 47
Procent.. 48
Rente. 49
Indeks. 50
Geometri 51
Areal af trekant 51
Vinkelsum i en trekant 51
Ens- vinklede trekanter. 51
Vilkårlig
trekant.. 51
Sinusrelationerne: 51
Cosinusrelationerne: 51
Ret- vinklet
trekant.. 52
(Pytha- goras,
Sinus, Cosinus og Tangens) 52
Hvornår bruges
hvilke formler ved trekantberegning ?. 53
Eksponenter.. 53
Logaritmer.. 54
Omvendt proportionalitet.. 54
Vækst.. 55
Lineær vækst.. 55
Eksponentiel vækst.. 55
Potens-vækst.. 55
Forord
Dette hefte er en del
af et interaktivt læresystem i matematik hf, og beregnet til at blive brugt på
en pc med Explorer koblet på Internettet (mahf.dk). Herved bliver det muligt at benytte diverse links
til E-opgaver, interaktive opgaver og til videoer. Sideløbende hermed kan det
være praktisk at benytte en papirudgave, som kan printes direkte fra mahf.dk.
På mahf.dk findes dette hefte både i HTML-format med
links og i et printvenligt PDF-format, hvor de fleste links er inaktive.
Videoerne bør ses i
brudstykker på kun nogle få minutter af gangen.
Besvarelser af E-opgaver
sendes automatisk via Internettet til læreren.
Med denne matematik-pakke
følger endvidere et elektronisk afleveringsark, RegneRobot med matematik-editor
og CAS , hvor elever/kursister kan besvare opgaver og også her automatisk få
sendt opgavebesvarelserne til læreren.
RegneRobot indeholder
en række faciliteter, der gør det lettere at besvare opgaver.
Indholdsfortegnelsen
kan benyttes som links.
Uanset hvor man er i
dokumentet, kan man komme til indholdsfortegnelsen ved at taste Ctrl+Home ,
PageDown , PageDown.
Søgning på bestemte
ord (svarende til stikordsregister) foretages ved at taste Ctrl+f
Denne udgave,
Matematik C interaktivt del 2 for hf version 6.5 adskiller sig kun i dette
forord fra 6.4 og fra 6.3 ved en lille omskrivning af lektion 16.
Denne
undervisningspakke er under stadig udvikling
Eventuelle forslag og
rettelser til denne pakke er velkomne på lyngbydata.dk/rettelser
Flere eksemplarer af
denne matematik-pakke kan bestilles via lyngbydata.dk/pakke
/Peter Sørensen
Link til
Indholdsfortegnelse
Udfør
følgende 6 punkter
1) Se: Video med
potens-funktioner
2) Læs om:
Rapportopgave: ”Mønt
falder ned”
Gå op i et hus med flere etager og lad med forsigtighed en mønt falde
ned fra et vindue.
Tag tid på faldtiden og beregn vinduets højde over jorden.
Rapporten skal ikke laves før, du når til punkt 6).
Rapporten skal bl.a. indeholde:
En beskrivelse af problemet og af huset.
Alternative løsningsmetoder med fordele og ulemper.
Valg af løsningsmetode med begrundelse.
Måleresultater og beregning.
Evaluering med bl.a. en omtale af anvendt matematik (ligning,
potensfunktion, osv.).
3) Læs:
Definition:
En funktion, der har en
regneforskrift af formen y
= b·xa ,
hvor b>0 og x>0, kaldes en potensfunktion.
a kan være et hvilket som helst tal forskelligt fra 0.
Hvis a<0 er funktionen aftagende.
Eksempel:
Hvis man lader en mønt falde
ned fra et højhus, kan faldet med
god tilnærmelse beskrives ved modellen y = 5·x2 , hvor x er antal sekunder efter, der er
blevet givet slip på mønten og y er antal meter, som mønten er faldet. I dette
eksempel er b=5 og a=2
b er y-værdien når x er 1
Hvis man kender 2
funktionsværdier, kan man finde en regneforskrift.
a kan beregnes ved formlen:
|
|
|
|
a =
|
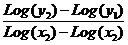
|
|
|
|
|
Herefter kan b findes ved hjælp af formlen:
Eks.
a = 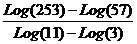 = 1,14704… = 1,1470
= 1,14704… = 1,1470
b = 57/3 ·1,14704… = 16,1657…
= 16,166
Regneforskriften bliver således: y = 16,166· x1,470
Fx
fås for x=25: y = 16,1657… · 251,4704… = 648,779…
= 648,78
Her har vi ikke brugt de afrundede værdier af a og b, men de mere
nøjagtige, som er gemt i lommeregner eller i regneark.
Lad os betragte
potens-funktionen: y = 7·x3
og lad os betragte en x-værdi og den tilsvarende y-værdi: 7·x3.
Vi vil nu fremskrive
x med 20%.
Dvs. x ganges med
fremskrivningsfaktoren (1+20%) = 1,20.
Den nye y-værdi
bliver 7·(x·1,20)3 =
7·x3 · 1,203
= y · 1,203
Altså: y skal
ganges med 1,203
= 1,728
hvilket er det samme
som at fremskrive y med (1,728 – 1) · 100% = 72,8%
Vi bemærker, at når x
fremskrives med faktoren 1,20,
så fremskrives y med faktoren 1,203
Eller sagt på en
anden måde:
Når x
fremskrives med 20%, så fremskrives y med (1,203 - 1) · 100%
Generelt gælder om en
potens-funktion:
Når x fremskrives
med faktoren (1+r) så
fremskrives y med faktoren (1+r)a
eller:
Når x fremskrives
med faktoren (1+p%) så
fremskrives y med faktoren (1+p%)a
Eller sagt på en anden måde:
Når x
fremskrives med p%, så fremskrives y med ((1+p%)a – 1) · 100%
Dvs, om en
potens-funktion gælder:
Når x vokser med en bestemt procent,
så vil y også vokse med en bestemt procent,
og ud fra den %-vise vækst af x kan man beregne den %-vise vækst af y.
Det modsatte gælder
også:
Enhver funktion, der har ovenstående egenskab, er en
potens-funktion.
Eksempel:
y=5000·x - 0,7
En
%-vis forøgelse af x med 30%
til (x ·1,30) giver
en ny y-værdi på 5000·(x·1,30) -0,7 = 5000·x - 0,7 · 1,30 -0,7
Altså
y forøges med faktoren 1,30 -0,7
svarende
til en %-vis forøgelse på (1,30 -0,7 - 1)·100 % = -16,77…% = -16,8%. (Det er en
aftagende funktion.)
Øveopgaver
Hvis man vil tegne en
potens-funktion kan man med fordel benytte et såkaldt dobbelt logaritmisk
koordinatsystem hvor tallene på både x-aksen og y-aksen er placeret således at
grafen for en potens-funktion bliver en ret linje.
Dobbelt logaritmisk koordinatsystem tegnes normalt i dobbelt logaritmisk papir eller ved hjælp af regneark.
Et koordinatsystem i Excel
regneark ændres til dobbelt logaritmisk koordinatsystem ved at klikke i et tal
på både x-aksen og y-aksen med højre musetast og begge gange vælge ”Formater akse.. ”
I Excel 97-2003 vælges derefter faneblad ”Skala” og der
sættes flueben i
Logaritmisk Skala.
Til sidst klikkes OK.
I Excel 2007 sættes blot flueben i Logaritmisk Skala.
Til sidst klikkes Luk.
Hvis støttepunkterne
i en tabel flugter en linje i et dobbelt logaritmisk koordinatsystem, kan man
konkludere, der med god tilnærmelse er tale om en potens-funktion.
Hermed
skulle været forklaret rigeligt til at kunne regne afleverings-opgaver.
4) Løs interaktiv øvelsesopgave potensfunktion
5) Løs E-opgaver: Link:
E-opgaver_15_Potens-funktion.htm
6) Løs og aflever rapportopgaven
”Mønt falder ned” i punkt 2)
og
opgaverne: 1.016, 1.017 , 1.018 i Vejledende eksamensopgaver
Se evt. video: Video om opg. 1.016
Link til Indholdsfortegnelse
Udfør
følgende 5 punkter
1) Se: Video med Statistik
2)
Læs:
Formålet med statistik er at få
overblik over et stort talmateriale.
Vi anvender nogle såkaldte deskriptorer, der beskriver
talmaterialet.
De enkelte tal i talmaterialet kaldes observationer.
Hele talmaterialet kaldes observationssættet
Vi vil her lærer betydningen af følgende såkaldte deskriptorer:
Mindsteværdi (den mindste observation)
Størsteværdi (Den største observation)
Middeltal (gennemsnit),
Median (midten
af observationerne, altså grænsen efter første halvdel)
Første kvartil eller nedre kvartil (Grænsen efter første
fjerdedel af observationerne)
Tredje kvartil eller øvre kvartil (Grænsen efter tredje
fjerdedel af observationerne)
Kvartilsæt (de 3 tal 1. kvartil, median og 3. kvartil)
Første kvartil og nedre kvartil er det samme. Ligeledes er tredje
kvartil lig øvre kvartil. Den præcise betydning af median, første kvartil og
tredje kvartil vil senere blive beskrevet.
Eksempel:
Vi betragter et selskab på 9 personer og deres vægte i kg:
55, 55, 60 , 61, 65, 70, 88, 90 og 95
Mindsteværdi: 55 kg
Størsteværdi: 95 kg
Middeltal: (55+55+60+61+65+70+88+90+95)kg / 9
Median:
65 kg
1. kvartil: 57,5 kg (Når der ikke er noget tal i midten, tager vi
midten af de 2 midterste tal)
3. kvartil: 89 kg
Kvartilsæt: 57.5 kg , 65 kg, 89 kg
En boksplot er en grafisk fremstilling af nogle
observationer.
Boksplotten viser mindsteværdien, de 3 kvartiler og
størsteværdien.
I en boksplot indgår et rektangel, hvor de to tider
angiver 1. og 3. kvartil.
Parellelt med disse sider er inde i rektanglet et
linjestykke, som viser 2. kvartil (medianen)
Vinkelret herpå, tværs gennem rektanglet, er et
linjestykke, hvis endepunkter viser mindste og størsteværdi.
Eksempel:
Der er et selskab på 7 mennesker med følgende aldre:
3, 5, 9, 10, 12, 14, 20
Mindsteværdien = 3
1. kvartil = 5
Median = 10
3. kvarttil = 14
Størsteværdien = 20
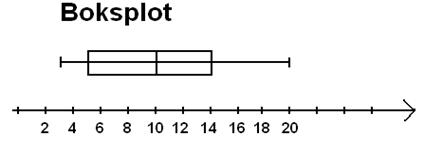
Få regneark til at tegne et
boksplot m m. Link: Boksplot
v. Jens Runge
Middeltallet, også
kaldet gennemsnittet, er summen af alle observationer divideret med antallet.
Hvis observationerne
er grupperet i intervaller, kan denne beregningsmetode ikke bruges. Vi vil
senere se, hvordan vi beregner middeltallet ved grupperede observationer.
Når der er mange
forskellige observationer vælger man ofte at gruppere observationerne, fx:
Bemærk, 0 à 29
svarer til intervallet [0;30[, fordi folk siger de 29 lige indtil blot én
dag før, de fylder 30. Denne særhed afspejles ved statistik med alder.
grupperede
observationer og ved ikke-grupperede observationer.
Vi ser ovenfor endnu
en deskriptor nemlig frekvens. Frekvensen
angiver hvor stor en brøkdel, der er i et interval i forhold til alle
observationer.
Frekvens
kan angives i % eller som decimalbrøk, fx 35% eller 0,35
Frekvensen
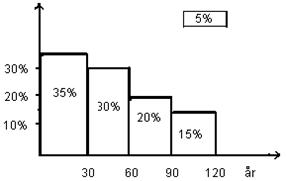
(eller hyppigheden) kan fremstilles grafisk i et såkaldt histogram:
HISTOGRAM
Skabelon til tegning
af histogram: Skabelon_histogram.xls
Middeltal ved grupperede observationer
Ved grupperede
observationer kan man ikke vide, hvordan observationerne fordeler sig i hvert
interval, men man har vedtaget at betragte det som om, de fordeler sig jævnt.
Ved beregning af
middeltallet kommer det ud på det samme, som at betragte det som om, alle
observationer i hvert interval ligger midt i intervallet.
Derfor beregnes
middeltallet ved for hvert interval at gange intervalmidtpunktet med
intervallets frekvens og derefter lægge alle produkterne sammen
I ovenstående
eksempel er intervalmidtpunkterne 15, 45, 75 og 105.
Middeltallet =
15·35% + 45·30% + 75·20% + 105·15% = 49,5
Der findes yderligere
nogle deskriptorer:
Kumuleret
hyppighed, der beregnes ved at lægge hyppigheder sammen.
Kumuleret frekvens, der beregnes ved at lægge frekvenser sammen.
Hvis frekvenserne er
afrundede tal, kan det være mere nøjagtigt i stedet at dividere kumuleret
hyppighed med antal observationer i alt.
Her ses et skema med
beregninger af kumuleret hyppighed og kumuleret frekvens:
h, f,
H og F er hyppigt anvendte forkortelser for hyppighed,
frekvens , kumuleret hyppighed og kumuleret frekvens.
Den kumulerede
frekvens F er en funktion, der fortæller hvor mange %,
der er under en bestemt alder. Fx ses at 65% er under 60 år.
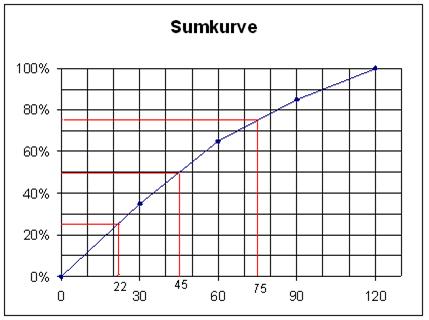
Grafen for denne
funktion kaldes en sumkurve og sumkurver tegnes altid med rette linjestykker
mellem støttepunkterne. De rette linjestykker er udtryk for, at man igen betragter
observationerne, som om de fordeler sig jævnt i hvert interval.
Median og
kvartiler defineres på én måde ved grupperede funktioner og på en anden måde
ved ikke grupperede observationer.
Observationerne
sorteres i stigende orden
Ved et ulige
antal observationer defineres medianen som den midterste observation.
Ved et lige
antal observationer defineres medianen som midtpunktet af de 2
midterste observationer.
Første kvartil eller 1. kvartil eller nedre kvartil defineres
som medianen for de observationer, der ligger til venstre for hele
observationssættets median.
Tredje kvartil eller 3. kvartil eller øvre kvartil defineres
som medianen for de observationer, der ligger til højre for hele
observationssættets median.
Ved
grupperede observationer aflæser vi kvartilsættet ved hjælp af sumkurven:
1. kvartil: Gå vandret fra 25% på 2.aksen til
sumkurven og så lodret til 1.aksen.
Medianen:
Gå vandret fra 50% på 2.aksen til
sumkurven og så lodret til 1.aksen.
3. kvartil: Gå vandret fra 75% på 2.aksen til
sumkurven og så lodret til 1.aksen.
-
Ved ovenstående
sumkurve bliver kvartilsættet: 22 år, 45 år, 75 år
Prøv skabelon til
tegning af sumkurve m.m. Link: Skabelon_sumkurve.xls
3) Løs Interaktiv statistik-opgave
4) Løs E-opgaver:
E-opgaver_16a_Statistik.htm
E-opgaver_16b_Statistik.htm
5) Løs afleveringsopgaver: 1.019, 1.020, 2.006, 2.016
i
Vejledende eksamensopgaver
Link til Indholdsfortegnelse
Lektion 17: Repetition og
flere beviser mv.
Udfør
følgende 5 punkter
1) Se videoerne:
Video om geometri med beviser
Lineære funktioner med_beviser
Potensfunktion
med beviser
2) Læs:
Arealet af en trekant er ½ højde gange
grundline
Vi bruger formlen: A=½h·g
Vi vil nu anskueliggøre formlen.
Betragt et rektangel
med samme grundlinje og højde:
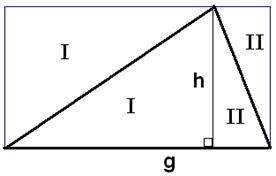
Firkantens areal er h·g
Vi ser De to områder
med 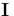 er lige store og de to områder med
er lige store og de to områder med  er
lige store.
er
lige store.
Derfor er arealet af
trekanten det halve af firekantens areal, altså : A=½h·g
Vinkler
|
Ensliggende
vinkler er lige store
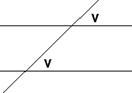
|
Topvinkler
er lige store
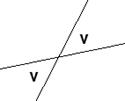
|
Det bevises
således:
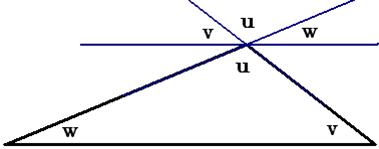
Ved trekantvinklen u er tegnet en linje parallel med modstående
side.
De to vinkler v er
lige store fordi det er ensliggende vinkler ved parallelle linjer.
Det samme gælder de
to vinkler w
De to vinkler u er
lige store, fordi de er topvinkler.
Herefter ses det
umiddelbart at vinkelsummen u + v + w = 180°
Bevis:
Vinkelsummen er lig
180° minus den rette vinkel på 90°, altså 180° – 90° = 90°
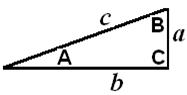
c² = a² + b²
Sagt med ord:
kvadratet på hypotenusen er lig summen af kateternes kvadrater
Pythagoras’s sætning kan
illustreres således:
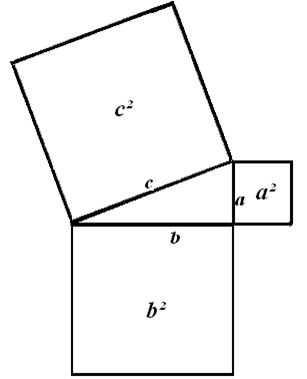
Det store kvadrat og de to
små har samme areal.
Her vil blive vist to
beviser af Pythagoras sætning.
Du behøver kun at
kunne det ene til mundtlig eksamen.
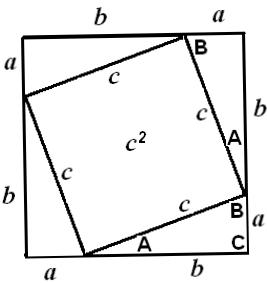 Bevis
1:
Bevis
1:
Vi betragter et
kvadrat med sidelængden a+b
Vi placerer 4 kopier
af den retvinklede trekant inde i kvadratet som vist på figuren.
Firkanten inde i
midten er et kvadrat fordi siderne er lige lange nemlig c og alle vinkler er 90°. Det er de fordi de sammen med
deres nabovinkler er 180° og nabovinklerne udgør 90°, nemlig de 2 spidse
vinkler i den retvinklede trekant.
Arealet af den store
firkant kan dels beregnes således:
(a+b)² =
(a+b)·(a+b) = a² + ab + ab + b² = a² + b² + 2ab
og dels således:
Arealet af det lille
kvadrat inden I midten plus arealet af de 4 trekanter
= c² + 4·½·a·b =
c² + 2ab
Altså c² + 2ab
= a² + b² + 2ab ó
c² = a² + b² hvilket skulle
vises.
Bevis
2:

Vinkel C er 90°
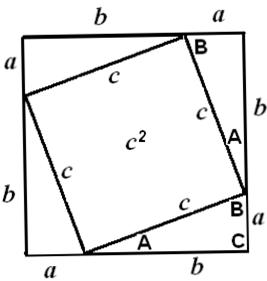
Denne retvinklede trekant
kopieres 4 gange over i et stort kvadrat med sidelængden a+b.
Se nedenfor til
venstre. Der opstår et kvadrat inde i midten med sidelængden c og arealet c².
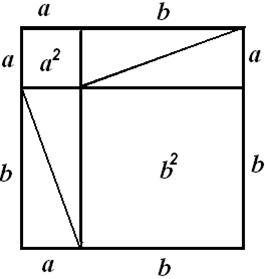
Det store kvadrat til
højre er magen til. Her indtegnes et lille kvadrat oppe i venstre hjørne med
sidelængden a og i nederste højre hjørne et kvadrat med
sidelængden b. Resten af det store kvadrat fyldes ud med 4
kopier af den forelagte retvinklede trekant.
Lighedstegnet mellem
de to figurer betyder, at de har samme areal.
|
|
=
|
|
Vi fjerner nu 4 trekanter
fra både figuren til venstre og fra figuren til højre, og vi får:
|
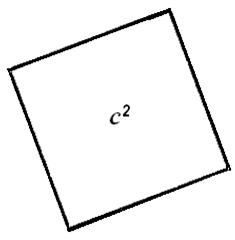
|
=
|
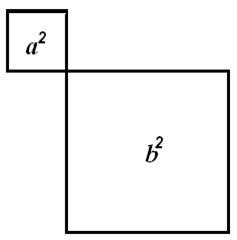
|
Man kan måske tvivle
på om firkanten til venstre nu også er et kvadrat.
Lad bevise at
firkanten er et kvadrat.
En firkant kaldes et
kvadrat, hvis alle sider er lige lange og alle vinkler er 90°.
1)
De 4 sider har alle
længden c og er således lige lange.
2)
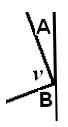 Vi betragter den
ene af vinklerne samt dens 2 nabovinkler.
Vi betragter den
ene af vinklerne samt dens 2 nabovinkler.
Vi skal bevise at v
= 90°
Vinkel A og B er de to spidse
vinkler i den oprindelige retvinklede trekant, og er tilsammen 90°.
Vinkel v må således være 90°, da summen af de 3vinkler er 180°
Et tilsvarende
argument gælder for de 3 andre firkantvinkler, og derfor er firkanten et
kvadrat.
Til enhver spids vinkel
kan vi knytte et tal, vi kalder sinus til vinklen og et tal , vi kalder cosinus
til vinklen.
Det gør vi på
følgende måde:
Lad os betragte en spids
vinkel v.
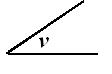
Den placerer vi i et
koordinatsystem således, at vinklens toppunkt ligger i koordinatsystemets begyndelsespunkt
og så højrebenet falder sammen med x-aksen.
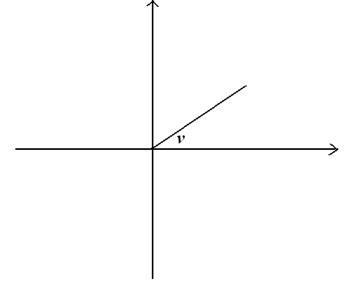
I koordinatsystemet
tegnes en cirkel med radius 1 og centrum i koordinatsystemets begyndelsespunkt.
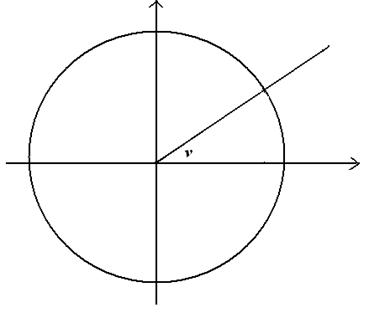
Fra skæringspunktet
mellem vinklens venstre ben og cirklen tegnes en lodret linje hen til x-aksen.
Det tal, som denne linje rammer kaldes Cos(v) eller blot Cos v. Det udtales cosinus til vinklen.
Endvidere tegnes fra
skæringspunktet en vandret linje hen til y-aksen. Det tal, som denne linje
rammer kaldes Sin(v) eller blot Sin v. Det
udtales sinus til vinklen.

Der er opstået en
retvinklet trekant med den ene katete langs x-aksen og da radius er 1, får denne
trekant en hypotenuse med længden 1.
En retvinklet trekant
med hypotenusen 1 kaldes en standardtrekant
Den til vinkel v hosliggende katete i standardtrekanten har længden Cos
v, og den modstående katete har længden Sin v.
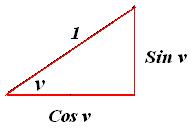
Vi betragter en
retvinklet trekant:
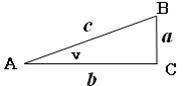
og en standardtrekant ensvinklet
med den forelagte: 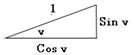
Vi skal bevise 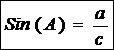
Skalafaktoren
(forstørrelsesfaktoren) fra standardtrekanten til den forelagte er c
|
og
|
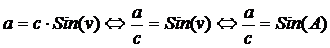
|
, hvilket skulle
vises
|
Cosinusformlen
bevises på tilsvarende måde.
Definition: 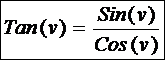
Formel: 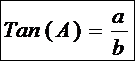
hvor bogstaverne
henviser til en retvinklet ΔABC med den rette vinkel i C
Bevis:
|
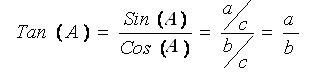
|
, hvilket skulle
bevises.
|
Bevis for Sinus-
og Cosinusrelationerne indgår
ikke i pensum på Matematik C
Definition:
En
funktion kaldes lineær, hvis grafen er en linje eller en del af en linje.
Her er 2 eksempler på
lineære funktioner:
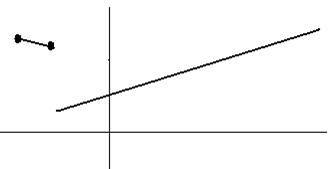
Den til venstre er
ikke defineret for x ≥ 0.
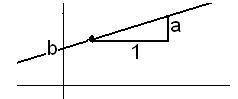 Begyndelsesværdien b er det
tal på y-aksen,
Begyndelsesværdien b er det
tal på y-aksen,
hvor grafen eller dens forlængelse skærer
y-aksen.
Hældningskoefficienten
a er den tilvækst, der kommer i y
når x gøres én større. Se tegning:
Formel:
Hvis man kender 2
punkter på grafen: (x1 , y1 ) og (x2 , y2)
kan a
beregnes, idet
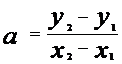
Bevis:
Vi vil kun gennemføre
beviset for en voksende funktion defineret for alle x. Dvs. grafen er en
opadgående linje.
Nedenfor ses en sådan
graf med de 2 grafpunkter markeret.
Endvidere er a markeret
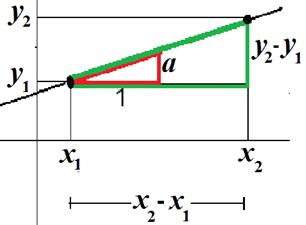
På tegningen optræder
2 ensvinklede trekanter, en rød og en grøn.
Skalafaktoren
(forstørrelsesfaktoren) fra den røde trekant til den grønne kan beregnes ved at
dividere tilsvarende sider.
Ved at dividere de 2
lodrette fås (y2 - y1)/a
Ved at dividere de 2
vandrette fås (x2-x1) / 1 = (x2-x1)
Altså (x2-x1)
= (y2
- y1)/a
ó a (x2-x1)
= (y2 - y1)
|
ó
|
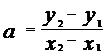
|
Hvilket skulle vises.
Regel
For en lineær
funktion gælder at regneforskriften er: y = ax + b
Bevis
Vi betragter et punkt
(x
, y) og vil finde en
formel for y.
Vi betragter
yderligere punktet (0, b)
Disse 2 punkter indsættes i
formlen for a og vi får
a = (y - b)/(x - 0) ó
a = (y - b) / x ó
ax = (y - b) ó
ax + b = y Hvilket skulle bevises
Formel: b = y1 - a x1
Bevis
y1 = a
x1 + b ó
y1 - a x1 = b Hvilket skulle bevises
Potensfunktioner
Definition: y=b·xa , b>0 og x>0
Der gælder:
Log y er en liner funktion af log x
Det ses ved at tage
log på begge sider af lighedstegnet.
Log y = Log (b·xa) Ved anvendelse af en af logaritmereglerne
fås
Log y = Log b
+Log (xa) Ved at anvende en anden
logaritmeregel fås
Log y = Log b +a
· Log x , som er
regneforskriften for en lineær
funktion
af Log x, idet begyndelsesværdien
er
Log b og hældningskoefficienten er a.
Grafen bliver en linje i
dobbelt logaritmisk
papir.
a kan findes ved at måle på grafen eller ved at aflæse to
|
grafpunkter og
bruge formlen:
|
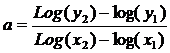
|
b findes ved 
Fremskrivning
af y med fremskrivningsfaktoren (1+r)
Vi betragter y1 = b·x1a
og fremskriver x1 fremskrivningsfaktoren (1+r)
Det giver en ny
x-værdi
x2 = x1·(1+r)
og en ny y-værdi y2 = b·( x1·(1+r))a
.
Ud fra reglerne om
regning med eksponenter fås:
y2 =
b·x1
a·(1+r)a og da y1
= b·x1a fås
y2 = y1·(1+r)a
Altså når x fremskrives
med faktoren (1+r) ,
så fremskrives y med (1+r)a
3) Løs E-opgaver:
Link:
E-opgaver_17_eksp
E-opgaver_14b_lineær_og_eksponentiel
funktion
E-opgaver_17_eksponentiel
funktion
Følgende e-opgaver
er med henblik på mundtlig eksamen.
E-opgaver 18a Mundtlig eksamen. Var.samh.
& grafer
E-opgaver 18b Mundtlig
eksamen. % & rente
E-opgaver 18c Mundtlig eksamen. Lineær vækst
E-opgaver 18d Mundtlig eksamen. Eksponentiel
vækst
E-opgaver 18e Mundtlig
eksamen. Potensfunktioner
E-opgaver 18f Mundtlig eksamen.
Trekantberegning
E-opgaver 18g Mundtlig eksamen. Statistik
4) Løs resten af opgaverne i Vejledende eksamensopgaver
Desuden anbefales ekstra terminsprøver
Link til
Undervisningsministeriets hjemmesider med prøvesæt:
http://us.uvm.dk/gymnasie/almen/eksamen/opgaver/matematik-ny.htm?menuid=150560 (Vælg C-niveau)
Terminsprøver bør udføres på 3 timer i ét stræk og uden
forstyrrelser.
Link til
Indholdsfortegnelse
Udfør 1) og 2)
1) Læs.
Pensum til mundtlig
eksamen er nedfældet i en undervisningsbeskrivelse. Både
undervisningsbeskrivelsen og eksamensspørgsmålene offentliggøres i god tid før
eksamen på skolens hjemmeside.
Eksempel på
undervisningsbeskrivelse
svarende til denne undervisningspakke:
Link: Undervisningsbeskrivelse
Eksempel på eksamens-spørgsmål:
1. Procent- og
rentesregning
Gør rede for begrebet
fremskrivningsfaktor.
Gør rede for
renteformlen for kapitalfremskrivning og for gennemsnitlig årlig rente, gerne
med udgangspunkt i et konkret eksempel.
2. Procent- og
rentesregning
Gør rede for begrebet
fremskrivningsfaktor.
Gør rede for
indekstal.
Gør rede for
renteformlen for kapitalfremskrivning
3.
Variabelsammenhænge og grafer
Gør rede for
variabelsammenhænge bestemt ved en regneforskrift og ved en graf.
Vis hvordan, man
tegner grafer, gerne med udgangspunkt i rapporten ”Temperatur” .
Vis et eksempler på
grafer for lineære funktioner og forklar betydningen af b i
regneforskriften: y=ax+b .
4.
Variabelsammenhænge og grafer
Gør rede for
variabelsammenhænge bestemt ved en regneforskrift og ved en graf.
Vis hvordan, man
tegner grafer, gerne med udgangspunkt i rapporten temperatur.
Gør rede for ligefrem
proportionalitet og for omvendt proportionalitet.
5. Lineær vækst
Definer lineær
funktion.
Du skal bl.a. komme
ind på betydningen af tallene a og b og på, hvordan a og b
kan bestemmes.
Bevis formlen for
a
6. Lineær vækst
Definer lineær
funktion
Du skal bl.a. komme
ind på betydningen af tallene a og b og på, hvordan a og b
kan bestemmes.
Bevis at
regneforskriften er 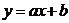 .
.
7. Eksponentiel
vækst
Gør rede for den
eksponentielle vækstmodel 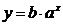 .
.
Du skal bl.a. komme
ind på betydningen af tallene a og b og på, hvordan a og b
kan bestemmes.
8. Eksponentiel
vækst
Gør rede for den
eksponentielle vækstmodel 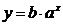 .
.
Du skal bl.a. komme
ind på enkeltlogaritmisk koordinatsystem.
9. Eksponentiel
vækst
Gør rede for den
eksponentielle vækstmodel 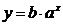 .
.
Du skal bl.a. komme
ind på bestemmelse af fordoblingstid og halveringstid.
10.
Potensfunktioner
Gør rede for
potensfunktionen 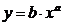 , gerne med udgangspunkt i rapporten: “Mønt
falder ned”.
, gerne med udgangspunkt i rapporten: “Mønt
falder ned”.
Du skal bl.a. komme
ind på betydningen af tallene a og b og på, hvordan a og b
kan bestemmes.
11.
Potensfunktioner
Gør rede for
potensfunktionen 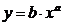 , gerne med udgangspunkt i rapporten: “Mønt
falder ned”.
, gerne med udgangspunkt i rapporten: “Mønt
falder ned”.
Du skal bl.a. komme
ind på dobbeltlogaritmisk koordinatsystem.
12.
Trekantsberegning
Gør rede for
ensvinklede trekanter, gerne med udgangspunkt i rapportopgaven ”Find højden”.
Gør rede for sinus og
cosinus i den retvinklede trekant.
Forklar og bevis
Pythagoras’ sætning.
13.
Trekantsberegning
Gør rede for
ensvinklede trekanter gerne med udgangspunkt i rapporten ”Find højden”.
Gør rede for sinus og
cosinus i den retvinklede trekant.
Bevis sinus- og cosinusformlerne
14.
Trekantsberegning
Gør rede for sinus,
cosinus og tangens i den retvinklede trekant.
Forklar og bevis
formlen for tangens
15. Statistik
(bilag vedlagt)
Gør rede for
kvartiler, både for et ikke grupperet og for et grupperet observationssæt.
Du skal desuden komme ind på begrebet boksplot.
Du må gerne tage
udgangspunkt i et eller to konkrete eksempler, eventuelt fra bilaget.
16. Statistik
(bilag vedlagt)
Gør rede for
kvartiler, både for et ikke grupperet og for et grupperet observationssæt. Du
skal desuden komme ind på begrebet sumkurve.
Du må gerne tage
udgangspunkt i et eller to konkrete eksempler, eventuelt fra
bilaget..
BILAG:
Eksempel 1:
Der er et selskab
på 7 mennesker med følgende aldre: 3, 5, 9, 10, 12, 14, 20
Eksempel 2
Link til Indholdsfortegnelse
Alle
hjælpemidler er tilladte, også andres notater, dog er kommunikation med
omverden ikke tilladt.
Under
eksaminationen bør man ikke kigge for meget i sine notater. Direkte oplæsning
eller afskrift fra notater vil ikke tælle positivt ved bedømmelsen.
Hvis man
går i stå under fremlæggelsen, kan man kigge i notaterne, men man bør holde
mund mens man kigger.
Mundtlig
eksamen er todelt.
Første
del er kursistens fremlæggelse (se nedenstående dispositioner og videoer)
Anden del
er samtale
Første del vil typisk vare over halvdelen af tiden 12 à 15 min.
Anden del vil typisk vare 5 à 10 min og tage udgangspunkt i kursistens
fremlæggelse. Samtalen kan ikke bevæge sig uden for hovedoverskriften.
Man forbereder sig
til mundtlig eksamen ved til hvert spørgsmål at udarbejde en disposition og et
foredrag.
Nogen af spørgsmålene
ligner hinanden og foredragene vil være næsten ens.
Man kan således nøjes
med at forberede ét foredrag til spørgsmål 1 og 2, og et foredrag til
spørgsmål 3 og 4, osv.
Der skal således
forberedes 7 foredrag.
Foredrag til procent
og rentesregning bør indeholde alle de emner, der er i spørgsmål 1 og spørgsmål
2 tilsammen og gerne lidt mere; men rækkefølgen er forskellig. Det er vigtigt,
at man først taler om de emner, der er nævnt i det spørgsmål man har trukket..
Derefter kan man tale om de andre emner, der hører under hovedoverskriften.
Tilsvarende med
Variabelsammenhænge og grafer og alle de andre spørgsmål.
Det er en fordel at
forberede foredrag med så mange emner som muligt, så man har rigeligt at
fortælle om.
Sørg for at kunne
alle 7 foredrag lige godt.
Man bør på forhånd
have afprøvet alle 7 foredrag som en slags generalprøve. Det er en god idé at
være nogen stykker, der træner sammen ved en tavle og skiftes til at holde
foredrag for hinanden.
Link til Indholdsfortegnelse
Fremskrivningsfaktor.
Kapitalfremskrivning
Gennemsnitlig årlig rente
Indekstal
Fremskrivningsfaktor.
Kapitalfremskrivning
Indekstal
Gennemsnitlig årlig rente
Regneforskrift
Graf.
Tegning af grafer.
Grafer for den lineære funktion: y=2x+3
Betydningen af b og a
Proportionalitet
Omvendt proportionalitet
Regneforskrift
Graf.
Tegning af grafer.
Proportionalitet
Omvendt proportionalitet
Grafer for den lineære funktion: y=2x+3
Betydningen af b og a
Definer lineær funktion.
Definer a og b
Formlen for a
Formlen for b
Bevis formlen for a
Regneforskriften y=ax+b
Bevis regneforskriften y=ax+b
Konklussion: Regneforskrift kan bestemmes ud
fra 2 grafpunkter
Definer lineær funktion.
Definer a og b
Bevis regneforskriften y=ax+b
Bevis formlen for a
Bevis formlen for b
Konklusion: Regneforskrift kan bestemmes ud
fra 2 grafpunkter
Definition af eksponentiel vækst 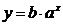 .
.
Betydningen af a og b
Formlen for a
Formlen for b
Bevis formlen for a
Bevis formlen ofr b
Konklusion: Regneforskrift kan bestemmes ud
fra 2 grafpunkter
Enkelt logaritmisk koordinatsystem
T2 og T½
Find T2 og T½ grafisk
Bevis formlerne for T2 og T½
Definition af eksponentiel vækst 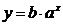 .
.
Betydningen af a og b
Enkelt logaritmisk koordinatsystem
T2 og T½
Find T2 og T½ grafisk
Bevis formlerne for T2 og T½
Formlen for a
Formlen for b
Bevis formlen for a
Bevis formlen ofr b
Konklusion: Regneforskrift kan bestemmes ud
fra 2 grafpunkter
Definition af eksponentiel vækst 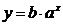 .
.
Betydningen af a og b
Enkelt logaritmisk koordinatsystem
T2 og T½
Find T2 og T½ grafisk
Bevis formlerne for T2 og T½
Formlen for a
Formlen for b
Bevis formlen for a
Bevis formlen for b
Konklusion: Regneforskrift kan bestemmes ud
fra 2 grafpunkter
Definition af potensfunktion 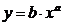 .
.
Betydningen af a og b
Formlen for a
Formlen for b
Bevis formlen for a
Bevis formlen for b
Dobbeltlogaritmisk koordinatsystem
11.
Potensfunktioner
Definition af potensfunktion 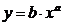 .
.
Betydningen af a og b
Dobbeltlogaritmisk koordinatsystem
Formlen for a
Formlen for b
Bevis formlen for a
Bevis formlen for b
Ensvinklede trekanter.
Højden af en flagstang el. Lign.
Definition af sinus og cosinus
Sin- og Cosinusformlerne
Forklar Pythagoras’ sætning.
Bevis Pythagoras’ sætning.
Bevis Sin- og Cosinusformlerne
Definer Tangens
Bevis tangensformlen
Eksempel på anvendelse af formlerne
Ensvinklede trekanter.
Højden af en flagstang el. Lign.
Definition af sinus og cosinus
Sin- og Cosinusformlerne
Bevis Sin- og Cosinusformlerne
Definer Tangens
Bevis tangensformlen
Forklar Pythagoras’ sætning.
Bevis Pythagoras’ sætning.
Eksempel på anvendelse af formlerne
Definition af sinus og cosinus
Sin- og Cosinusformlerne
Definer Tangens
Bevis tangensformlen
Bevis Sin- og Cosinusformlerne
Forklar Pythagoras’ sætning.
Bevis Pythagoras’ sætning.
Ensvinklede trekanter.
Eksempel på anvendelse af formlerne
15.
Statistik
Fortæl om formål med statistik
Betragt observationssættet: 3, 5, 9, 10, 12, 14, 20
Definer median
Definer nedre kvartil
Definer øvre kvartil
Definer mindsteværdi og størsteværdi
Tegn et boksplot
Middeltal = gennemsnit (3+5+9+10+12+14+20)/7
= 10,4… = 10
Betragt følgende observationssæt for
grupperede observationer
|
Alder:
|
[ 0; 30 [
|
[ 30;
60 [
|
[60 ;
90 [
|
[ 90 ;
120 [
|
|
h Antal
(hyppighed)
|
3500
|
3000
|
2000
|
1500
|
|
H kumuleret
hyppighed
|
3500
|
6500
|
8500
|
10000
|
|
f frekvens
|
3500/10000
= 35%
|
3000/10000
= 30%
|
2000/10000
= 20%
|
1500/10000
= 15%
|
|
F kumuleret
frekvens
|
3500/10000 = 35%
|
6500/10000
= 65%
|
8500/10000
= 85%
|
100%
|
Tegn sumkurven ud fra støttepunkterne:
|
Alder:
|
0
|
30
|
60
|
90
|
120
|
|
F
|
0%
|
35%
|
65%
|
85%
|
100%
|
Definer median
Definer nedre kvartil
Definer øvre kvartil
Definer middeltal (Sum af interval-midtpunkt gange frekvens: 15·0,35
+ 45·0,30 + 75·0,20 + 105·0,15 = 49,5)
Fortæl om forskel på median og middeltal
Tegn histogram
Fortæl om formål med statistik
Betragt observationssættet: 3, 5, 9, 10, 12, 14, 20
Definer median
Definer nedre kvartil
Definer øvre kvartil
Definer mindsteværdi og størsteværdi
Middeltal = gennemsnit (3+5+9+10+12+14+20)/7
= 10,4… = 10
Betragt følgende observationssæt for
grupperede observationer
|
Alder:
|
[ 0; 30 [
|
[ 30;
60 [
|
[60 ;
90 [
|
[ 90 ;
120 [
|
|
h Antal
(hyppighed)
|
3500
|
3000
|
2000
|
1500
|
|
H kumuleret
hyppighed
|
3500
|
6500
|
8500
|
10000
|
|
f frekvens
|
3500/10000
= 35%
|
3000/10000
= 30%
|
2000/10000
= 20%
|
1500/10000
= 15%
|
|
F kumuleret
frekvens
|
3500/10000 = 35%
|
6500/10000
= 65%
|
8500/10000
= 85%
|
100%
|
Definer median
Definer nedre kvartil
Definer øvre kvartil
Definer middeltal (Sum af interval-midtpunkt gange frekvens: 15·0,35
+ 45·0,30 + 75·0,20 + 105·0,15 = 49,5)
Fortæl om forskel på median og middeltal
Tegn histogram
Tegn et boksplot
Link til
Indholdsfortegnelse
|
Opg.
1001
|
|
|
|
|
|
|
|
|
Værdien
af maleriet efter 5 år:
|
60000
kr *1,12^5 =
|
105.740,50
|
kr
|
|
|
Den
11-årige fremskrivningsfaktor (1+r)^11 =
|
125000/85000
=
|
1,470588
|
|
|
Gennemsnitlig
årlig fremskrivningsfaktor:
|
(1+r)
=
|
1,47…^(1/11)
=
|
1,035682
|
|
|
Gennemsnitlig
årlig %-vis vækst: r =
|
1,035…-1
=
|
3,57%
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1002
|
|
|
|
|
|
|
|
|
Antal
år fra 1960 til 2000:
|
2000-1960
= 40
|
|
|
|
|
Gennemsnitlig
årlig vækst af befolkningstallet: (29,986/8,157)^(1/40)-1=
|
3,31%
|
|
Antal
år fra 2000 til 2010:
|
2010-2000
= 10
|
|
|
|
|
Prognosen
viser en befolkning i 2010 på:
|
29,986*1,025^10
mio =
|
38,385
|
mio
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.003
|
|
|
|
|
|
|
|
A
= 4 · π · r²
|
|
|
|
|
|
|
|
Ved
at indsætte 1000 i stedet for A fås:
|
|
|
|
|
|
1000
= 4 · π · r² <=> 1000/(4·π) = r²
|
|
|
|
|
|
<=>
r² =
|
79,57747
|
|
|
|
|
|
|
|
<=>
r =
|
8,920621
|
|
|
|
|
|
|
|
DVS radius er 8,9 cm
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.004a
|
|
|
|
|
|
|
|
Jeg
indsætter i formlen og får:
|
|
|
|
|
|
|
BMI = 68/1,66² =
|
24,677021
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.004b
|
|
|
|
|
|
|
|
Også
her indsætter jeg i formlen og her får jeg, idet x betegner vægt i kg:
|
|
|
22
= x/1,71² <=> 22·1,71² = x <=>
|
64,3302
|
= x
|
|
|
|
Personens vægt er 64,33 kg
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.005
|
|
|
|
|
|
|
|
Jeg
vil beskrive den linæere model ved en regneforskrift y= ax+b
|
|
|
|
y
er befolkningen i millioner og x er antal år efter 1911 (regnet med fortegn)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Støttepunkter:
|
|
|
|
|
|
|
|
Årstal
|
1911
|
1950
|
|
|
|
|
|
|
x
|
0
|
39
|
|
|
|
|
|
|
y
|
1,003076
|
1,610123
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b
= 1,003
|
(svarende til x=0)
|
|
|
|
|
|
|
a
= (y2-y1) / (x2 - x1) =
|
0,0156
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x) = 0,0156x + 1,003
|
|
|
|
|
|
|
|
Dm(f)
= [-11; 54]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.006
|
|
|
|
|
|
|
|
Antal
sendte sms'er:
|
(486-630·0,70)/0,20
=
|
225
|
|
|
|
|
x
betyder antal sms'er og t betyder antal minuuter samtale
|
|
|
|
SMS'er
plus samtaler koster:
|
0,20x+0,70t
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Link til Indholdsfortegnelse
|
Opg. 1.007
|
|
|
|
|
|
|
Prisen
for 1 sms fås ved at sætte x=1 og t = 0
|
|
|
|
B
= 0,30·1 + 0,70·0 = 0,30
|
|
|
|
|
|
Prisen
for en sms er 30 øre
|
|
|
|
|
|
Minutprisen
for samtaler fås ved at sætte x=0 og t =1:
|
|
|
|
B
= 0,30·0 + 0,70·1 = 0,70
|
|
|
|
|
|
Minutprisen
for samtaler er 70 øre
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.008
|
|
|
|
|
|
|
B
= V / H²
|
|
|
|
|
|
|
|
Ved
at indsætte i denne formel fås
|
|
|
|
|
23
= V / 1,80² ó
V =
|
23*1,80²
ó V =
|
74,52
|
|
|
|
|
Personens vægt er 74,52 kg
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.009
|
|
|
|
|
|
|
p
og V er omvendt proportionale.
|
|
|
|
|
|
Dvs
p*V = k hvor k er konstant
|
|
|
|
|
|
Af
tabellens 2. kollonne fås k = 4*20 = 80
|
|
|
|
|
i
1. kollonne fås V = 80/2=40
|
|
|
|
|
|
i
3. kollonne fås p = 80/16=5
|
|
|
|
|
|
Den
udfyldte tabel se således ud:
|
|
|
|
|
|
p
|
2
|
4
|
5
|
|
|
|
|
V
|
40
|
20
|
16
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1010
|
|
|
|
|
|
|
|
0,218
er stigning i modstand målt i ohmnår temperaturen forøges 1 grad celcius.
|
|
56
er modstanden i ohm ved 0°C
|
|
|
|
|
|
Jeg
indsætter 65 i stedet foir y og får
|
|
|
|
|
65
= 0,218x+56 <=>
|
9 = 0,218x
<=> x =
|
41,2844
|
|
|
|
Ved
modstanden 65 ohm er temperaturen 41,3°C
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.011
|
|
|
|
|
|
|
-2600
fortæller at antallet af landbrug falder med 2600 om året
|
|
|
98680
fortæller at der i 1983 svarede til x=0 var 98680 landbrug
|
|
|
2010
svarer til x=27
|
|
|
|
|
|
|
Udfra
modellen beregnes antal landbrug i 2010 til: -2600*27+98680 =
|
28480
|
|
Jeg
vil nu finde det x hvor antal landbrug er 40 000 i henhold til modellen
|
|
40000
= -2600x + 98680 <=>
|
|
|
|
|
|
2600x
= 98680-40000 <=>
|
|
|
|
|
|
2600x
= 58680 <=>
|
|
|
|
|
|
x =
|
22,56923
|
|
|
|
|
|
|
Dvs
der vl gå 23 år før antal landbrug kommer under 40000
|
|
|
Det
bliver i året: 1983+23 =
|
2006
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.012
|
|
|
|
|
|
|
|
|
Støttepunkter:
|
|
|
|
|
|
|
|
|
x
|
20
|
80
|
|
|
|
|
|
|
|
y
|
16,3
|
34,6
|
|
|
|
|
|
|
|
a
= (34,6-16,3) / (80-20) =
|
0,305
|
|
|
|
|
|
|
b
= 16,3 - 20·a =
|
10,2
|
|
|
|
|
|
|
|
Ved
24,5 cm er loddets vægt x bestemt ved:
|
|
|
|
|
|
|
24,5
= ax + b
|
<=>
|
|
|
|
|
|
|
|
24,5
- b =
|
ax
|
<=>
|
|
|
|
|
|
|
|
(24,5-b)/a
=
|
x
|
<=>
|
|
|
|
|
|
|
|
46,89
|
=
x
|
|
|
|
|
|
|
|
|
Dvs loddet vejer 46,89 g
|
|
|
|
|
|
|
|
Hvis
der hænges yderligere 8,0 g på ændres fjederens position: 8,0·a=
|
2,44
|
cm
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg 1.013
|
|
|
|
|
|
|
|
|
Fra
1986 til 1998 er 12 år
|
|
|
|
|
|
|
|
Fra
1998 til 2010 er også 12 år
|
|
|
|
|
|
|
Hvis
udgifterne vokser linert fås:
|
|
|
|
|
|
|
|
Væksten
i en 12-års periode er 88,5 mia - 43,8 mia =
|
44,7
|
mia
|
|
|
|
Udgifter
til undervisning i 2010:
|
88,5
mia + 44,7 mia =
|
133,2
|
mia
|
|
|
|
Hvis
udgifterne vokser eksponentielt fås:
|
|
|
|
|
|
|
12-årig
fremskrivningsfaktor: (88,5 / 43,8)
|
|
|
|
|
|
Udgifter
til undervisning i 2010:
|
88,5
* (88,5 / 43,8) =
|
178,8
|
mia
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.014
|
|
|
|
|
|
|
|
|
Det
er en eksponentielt aftagende funktion med regneforskriften y=b·a^x
|
|
|
|
hvor
y er trykket i hektopascal og x er højden over jorden i km
|
|
|
|
|
a
= (1-11,5%) = 0,885
|
|
|
|
|
|
|
|
|
b=
1020
|
|
|
|
|
|
|
|
|
|
y
= 1020*0,885^x
|
|
|
|
|
|
|
|
|
Trykket
1,5 km over jordoverfladen: 1020*0,885^1,5 hektoåascal =
|
849,21
|
hektopascal
|
|
|
Hvis
trykket er 750 hektopascal fås:
|
|
|
|
|
|
|
1020*0,885^x
= 750
|
|
|
ó
|
|
|
|
|
|
0,885^x = 750
|
/
1020
|
|
ó
|
|
|
|
|
|
x*Log(0,885)
= Log(750/1020)
|
|
ó
|
|
|
|
|
|
|
x
= Log(750/1020) / Log(0,885)
|
ó
|
|
|
|
|
|
|
x
=
|
2,517
|
|
|
|
|
|
|
|
Dvs
trykket er 750 hektopascccal i en højde på 2,517 km
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Link til Indholdsfortegnelse
|
ALTERNATIV
LØSNINGSMETODE:
|
|
|
|
|
|
|
|
Opg. 1.014
|
|
|
|
|
|
|
|
|
Fremskrivningsfaktor
svarende til en forøgelse af højden på 1 km: (1-11,5%) = 0,885
|
|
|
Trykket
ved jordoverfladen: 1020 hektopascal
|
|
|
|
|
|
|
Trykket
1,5 km over jordoverfladen: 1020*0,885^1,5 hektoåascal =
|
849,21
|
hektopascal
|
|
|
h
angiver højden i km, hvor trykket er 750 hektopascal.
|
|
|
|
|
|
Der
må gælde: 1020*0,885^h = 750
|
|
|
|
|
|
|
|
0,885^h
|
=
|
750/1020
|
|
|
ó
|
|
|
|
|
Log(0,885^h)
=
|
Log(750/1020)
|
|
ó
|
|
|
|
|
h*Log*(0,885)
=
|
Log(750/1020)
|
|
ó
|
|
|
|
|
h
|
=
|
Log(750/1020)
/
|
Log(0,885)
|
ó
|
|
|
|
|
h
|
=
|
2,517
|
|
|
|
|
|
|
|
Dvs trykket er 750 hektopascccal i en højde på 2,517 km
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.015
|
|
|
|
|
|
|
|
|
Jeg
aflæser på grafen
|
|
|
|
|
|
|
|
|
x
|
0
|
6
|
|
|
|
|
|
|
|
y
|
20
|
40
|
|
|
|
|
|
|
|
Da
40 er det dobbelte af 20 er fordonlingstiden (6-0) =
|
6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.016
|
|
|
|
|
|
|
|
|
En
tilvækst i x på 11% forøger y med1,11^2,56-1 =
|
30,6%
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.0017
|
|
|
|
|
|
|
|
|
Hvis
indtagelsen af frugt og grønt forøges med 20%,
|
|
|
|
|
|
så
vil det årlige antal kræftdødsfald i danmark stige med 1,20^(-0,5)-1 =
|
-8,7%
|
|
|
|
DVS
antal kræftdødsfald vil være 8,7% mindre
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.018
|
|
|
|
|
|
|
|
|
442
er indiens befolkningstal i mio i 1961
|
|
|
|
|
|
|
1,0217
er den faktor befolkningstallet fremskrives med hvert år.
|
|
|
|
|
Dvs
befolkningen forøges med 2,17% hver år.
|
|
|
|
|
|
Befolkningstallet
= 884 mio
|
<=>
|
|
|
|
|
|
|
442·1,0217^x
= 884
|
|
<=>
|
|
|
|
|
|
|
1,0217^x
= 2
|
|
<=>
|
|
|
|
|
|
|
x·Log
1,0217 = Log 2
|
|
<=>
|
|
|
|
|
|
|
x
=
|
Log
2 / Log 1,0217
|
|
|
|
|
|
|
|
x
=
|
32,2876
|
|
|
|
|
|
|
|
|
Befolkningstallet
var 884 mio i året 1961+32=
|
1993
|
|
|
|
|
|
Året
2004 svarer til x = 2004 -1961 =
|
43
|
|
|
|
|
|
Befolkningstal
i 2004:
|
442mio*1,0217^43
=
|
1112,6
|
mio
|
|
|
|
|
Modellen
har været heldig, da 1112,6 mio er relativt tæt på det faktiske
|
|
|
|
beolkningstal
1100 mio og hvis man afrunder 1112,6 mio fås faktisk 1100 mio
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Link til Indholdsfortegnelse
|
Opg. 1.019
|
|
|
|
|
|
|
|
Af
sumkurven ses, at 78% af de ledige var under 55 år, Se bilag (som dog
ikke er med her)
|
|
Også
af sumkurven ses at under 40 år var:
|
50%
|
|
|
|
|
og
under 30 år var:
|
|
|
20%
|
|
|
|
|
Mellem
30 og 40 år var (50% - 20% ) =
|
30%
|
|
|
|
|
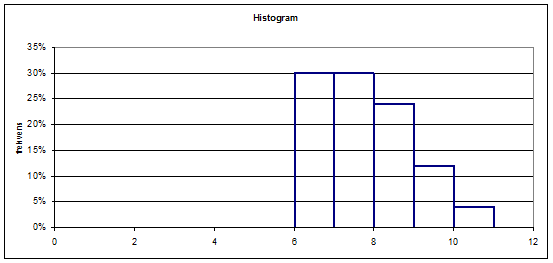
Opg. 1.020
|
|
|
|
|
|
|
|
|
Venstre intervalgrænse
|
6,0
|
7,0
|
8,0
|
9,0
|
10,0
|
|
Højre interavlgrænse
|
|
7,0
|
8,0
|
9,0
|
10,0
|
11,0
|
|
Hyyppighed h
|
|
15
|
15
|
12
|
6
|
2
|
|
Kumuleret hyppighed H
|
15
|
30
|
42
|
48
|
50
|
|
Frekvens f
|
|
30%
|
30%
|
24%
|
12%
|
4%
|
|
Kumuleret frekvens F
|
|
30%
|
60%
|
84%
|
96%
|
100%
|
|
|
|
|
|
|
|
|
|
|
Intervalmidtpunkt
|
6,5
|
7,5
|
8,5
|
9,5
|
10,5
|
|
Interval-midtpunkt gange frekvens:
|
2,0
|
2,3
|
2,0
|
1,1
|
0,4
|
|
Middeltal =
summen af ovenstående:
|
|
|
|
7,8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
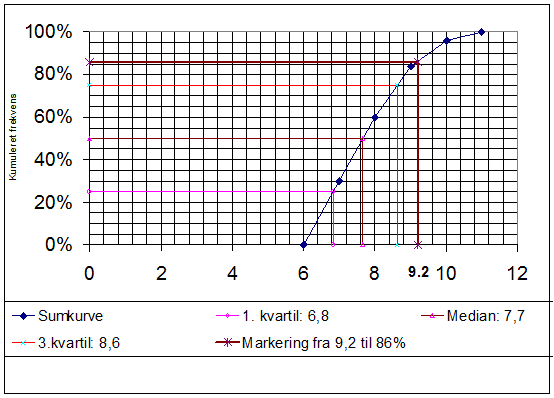
På
grundlag af kumuleret frekvens tegnes sumkurven:
|
|
|
|
|
|
|
|
|
|
Af
sumkurven aflæses øvre kvartil = 8,6
|
|
|
|
|
|
|
Ligeledes
ses at 85% havde et eksamensresultat på under 9,2
|
|
|
|
|
|
|
|
|
|
Dvs 15% havde et eksamensresultat på 9,2 eller derover.
|
|
|
|
|
|
|
|
|
Histogram tegnes ud fra frekvenserne f:
|
Opgave 1.021
|
|
|
|
|
|
|
|
|B'C'|
= (6/4) * 3 =
|
4,5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.022
|
|
|
|
|
|
|
|
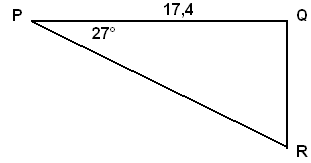
Ved
hjælp af Paint i Windows har jeg tegnet:
|
|
|
|
|
|
(for
at få billedet fra Paint kopieret over, måtte jeg først kopiere til Word)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q
= 17,4 / cos(27°) =
|
19,5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.023
|
|
|
|
|
|
|
|
Sin A = 4,5 / 8,3 =
|
|
0,5421687
|
|
|
|
|
|
|
Vinkel A = 33°
Vinkel B = 90°
|
|
|
|
|
|
|
|
Vinkel
A = 57°
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Link til Indholdsfortegnelse
|
Opg.
1.024
|
|
|
|
|
|
|
|
Cos
A = 3/5
|
=
|
0,6
|
|
|
|
|
|
|
Vinkle
A =
|
53
|
°
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
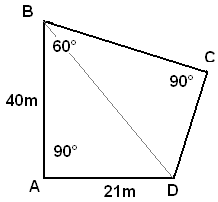
Opg. 1.025
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|BD| =
|
(21^2 + 40^2)^(1/2)m =
|
45,177…m
|
=
|
45,18m
|
|
|
|
Tan(vinkel
B i trekant ABD):
|
21 / 40 =
|
0,525
|
|
|
|
|
Vinkle
B i trekant ABC:
|
27,699
|
°
|
|
|
|
|
Vinkle
B i trekant BCD:
|
60° - 27,699° =
|
32,301
|
°
|
|
|
|BC| = 45,177...·cos 32,301…° =
|
38,187
|
|
|
|
|
|
|CD| = 45,177...·sin 32,301…° =
|
24,141
|
|
|
|
|
|
Byggegrundens areal = 0,5*40 * 21 + 0,5 *
38,187…* 24,141… =
|
881
|
m²
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Eksponenten
² fås ved at taste Alt+253 på num. Tastatur)
|
|
|
|
|
(Grader
° fåsved at taste Alt + 248)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 1.026
|
|
|
|
|
|
|
|
|AC|
= 5,0*sin 34,0° =
|
2,7960
|
|
|
|
|
|
|CB|
= 5,0·cos 34,0° =
|
4,1452
|
|
|
|
|
|
Trekantens
areal: 0,5·2,79… · 4,14… = 5,8
|
5,8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Link til Indholdsfortegnelse
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 2001
|
|
|
|
|
|
|
|
|
|
|AB|
=
|
Kvadratrod(12²+5²)
=
|
13
|
|
|
|
|
|
|
Skalafaktor:
|
13
/ 6,5 =
|
|
2
|
|
|
|
|
|
|
|DF|
=
|
5
/ 2 =
|
|
2,5
|
|
|
|
|
|
|
Opg. 2002
|
|
|
|
|
|
|
|
|
|
Punkterne
P og Q:
|
|
|
|
|
|
|
|
|
x
|
2
|
8
|
|
|
|
|
|
|
|
y
|
3
|
-1
|
|
|
|
|
|
|
|
a
=
|
(-1-3)
/ (8 - 2) =
|
- 2/3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
opg. 2003
|
|
|
|
|
|
|
|
|
|
Jeg
indsætter de anførte værdier i formlen og får:
|
|
|
|
|
|
|
500
= ½·a·17² <=>
|
|
|
|
|
|
|
|
1000
= a·17² <=>
|
|
|
|
|
|
|
|
1000
/ 17² = a
|
|
|
|
|
|
|
|
|
a =
|
3,460
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 2004
|
|
|
|
|
|
|
|
|
|
Af
grafen, bilag A, ses at, energibehovet for en vade fugl på 140g er 210
kJ/døgn
|
|
|
|
|
|
|
|
|
I
bilaget har jeg tegnet markering lodret ved 140 på 1. aksen og fra det punkt,
hvor denne markering
|
|
skærer
grafen har jeg tegnet en markering hen til 2.aksen og der aflæst de 210
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 2005
|
|
|
|
|
|
|
|
|
|
Stigens
højde op ad muren betegnes x
|
|
|
|
|
|
|
Sin
62° = x / 7,5 <=>
|
|
|
|
|
|
|
|
7,5·Sin
62° = x
|
|
|
|
|
|
|
|
|
x
=
|
6,622
|
…
|
|
|
|
|
|
|
|
Stigen
når 6,62m op ad muren
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 2006
|
|
|
|
|
|
|
|
|
|
De
15 priser i kr er:
|
|
|
|
|
|
|
|
|
Pris
|
1
|
7,55
|
|
|
|
|
|
|
|
Pris
|
2
|
7,95
|
|
|
|
|
|
|
|
Pris
|
3
|
7,95
|
|
|
|
|
|
|
|
Pris
|
4
|
7,95
|
|
|
|
|
|
|
|
Pris
|
5
|
7,98
|
|
|
|
|
|
|
|
Pris
|
6
|
7,98
|
|
|
|
|
|
|
|
Pris
|
7
|
8,05
|
|
|
|
|
|
|
|
Pris
|
8
|
8,15
|
|
|
|
|
|
|
|
Pris
|
9
|
8,25
|
|
|
|
|
|
|
|
Pris
|
10
|
8,55
|
|
|
|
|
|
|
|
Pris
|
11
|
8,55
|
|
|
|
|
|
|
|
Pris
|
12
|
8,75
|
|
|
|
|
|
|
|
Pris
|
13
|
8,95
|
|
|
|
|
|
|
|
Pris
|
14
|
8,95
|
|
|
|
|
|
|
|
Pris
|
15
|
9,05
|
|
|
|
|
|
|
|
Sum
|
:
|
124,61
|
|
|
|
|
|
|
|
Middeltallet
fås ved at dividere ovenstående sum med 15:
|
8,31
|
|
|
|
|
Det
ses priserne er i stigende orden
|
|
|
|
|
|
|
|
Medianen er den midterste pris, altså den 8.:
|
|
8,15
|
|
|
|
|
Af
figuren i bilaget ses, at den største pris er uændret, men
|
|
|
|
|
|
|
|
|
at
75% af priserne er faldet til under den oprindelige mindste pris.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 2007
|
|
|
|
|
|
|
|
|
|
x
betegner turens længde i km
|
|
|
|
|
|
|
|
y
betegner turens pris i kr
|
|
|
|
|
|
|
|
y = 10,55x + 33,00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hvis
prisen er 200 kr fås:
|
|
|
|
|
|
|
|
200
= 10,55x + 33,00
|
<=>
|
|
|
|
|
|
|
|
200
- 33,00 = 10,55x
|
<=>
|
|
|
|
|
|
|
|
167
|
=
10,55x
|
<=>
|
|
|
|
|
|
|
|
15,829
|
=
x
|
|
|
|
|
|
|
|
|
DVS
for 200 kr kan man køre 15,829 km
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 2008
|
|
|
|
|
|
|
|
|
|
Lysintensitet
i 2,5 m dybde:
|
100·0,69^2,5
=
|
39,55
|
|
|
|
|
Halveringskonstanten:
|
|
Log
0,5 / log 0,69 =
|
1,87
|
|
|
|
|
Dvs
at lysintensisteten halveres hver gang dybden forøges med 1,87 m
|
|
|
|
En
forøgelse på 1,0m betyder at lysintensiteten aftager med (1-0,69)·100% =
|
31%
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opg. 2009
|
|
|
|
|
|
|
|
|
|
Indeks
for basisåret 1998 er 100
|
|
|
|
|
|
|
|
Indeks for året 2003 er:
|
|
100
· 25708/22066 =
|
117
|
|
|
|
|
Fremskrivningsfaktor
1998 - 2003
|
for
månedsløn:
|
25708/22066
=
|
1,17
|
|
|
Fremskrivningsfaktor
1998 - 2003
|
for
husprisen:
|
173,3
/ 134,4 =
|
1,29
|
|
|
Dvs
husprisen er steget stærkest.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Link til Indholdsfortegnelse
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opgave 2010
|
|
|
|
|
|
|
|
|
|
Proportionalitetsfaktor:
9/2 =
|
4,5
|
|
|
|
|
|
|
x
|
2
|
3
|
4
|
10
|
|
|
|
|
|
y
|
9
|
13,5
|
18
|
45
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opgave 2011
|
|
|
|
|
|
|
|
|
|
|BC|
= 32,9 * sin(52) =
|
25,9
|
|
|
|
|
|
|
|AC|
= 32,9 * cos(52) =
|
20,3
|
|
|
|
|
|
|
Arealt
af trekant ABC: 0,5 * |BC| * |AC| =
|
262,6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opgave 2012
|
|
|
|
|
|
|
|
|
|
x
|
0
|
5
|
|
|
|
|
|
|
|
y
|
53500
|
88400
|
|
|
|
|
|
|
|
b = 53500
|
(svarende til x=0)
|
|
|
|
|
|
|
|
a
= (88400 - 53500) / (5-0) =
|
6980
|
|
|
|
|
|
|
b er antal golfspillere i 1992
|
|
|
|
|
|
|
a er stigningen i antal golfspillere pr år
|
|
|
|
|
|
|
2004
svarer til x = 2004 - 1992 = 12
|
|
|
|
|
|
|
Antal
golfspillere i 2004: 6980 * 12 + 53500 =
|
137260
|
|
|
|
|
|
Man
må sige væksten har været større efter 2001 end svarende til den linere model
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opgave 2013
|
|
|
|
|
|
|
|
|
|
3(x+1)
+ 4 = 27 - x
|
<=>
|
|
|
|
|
|
|
|
3x
+ 3 + 4 = 27 - x
|
<=>
|
|
|
|
|
|
|
|
4x
= 20
|
|
<=>
|
|
|
|
|
|
|
|
x = 5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opgave 2014
|
|
|
|
|
|
|
|
|
|
Saldo
efter 12 år: 15000 kr *1,0256^12 =
|
20315,49
|
kr
|
|
|
|
|
I
% er vokser beløbet på 5 år: (1,0256^5 - 1) * 100% =
|
13,47%
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opgave 2015
|
|
|
|
|
|
|
|
|
|
På
grafen aflæses:
|
|
|
|
|
|
|
|
|
x
|
2
|
6,5
|
|
|
|
|
|
|
|
y
|
8
|
4
|
|
|
|
|
|
|
|
Det
bemærkes at y halveres når x vokser fra 2 til 6,5
|
|
|
|
|
|
Halveringskonstanten
= 6,5 - 2 =
|
4,5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opgave 2016
|
|
|
|
|
|
|
|
|
|
Aldersfordeling, og højre intervalgrænse er her den alder,
|
|
|
|
|
der lige akurat overstiger alle aldre i intervallet.
|
|
|
|
|
|
|
Fx ved "5-19",er højre ingtervalggrænse være 20
|
|
|
|
|
|
Venstre intervalgrænse
|
15
|
20
|
25
|
30
|
35
|
40
|
|
Højre interavlgrænse
|
20
|
25
|
30
|
35
|
40
|
45
|
|
Frekvens f
|
1,9%
|
16,2%
|
37,7%
|
32,2%
|
10,5%
|
1,5%
|
|
Kumuleret frekvens F
|
1,9%
|
18,1%
|
55,8%
|
88,0%
|
98,5%
|
100,0%
|
|
|
|
|
|
|
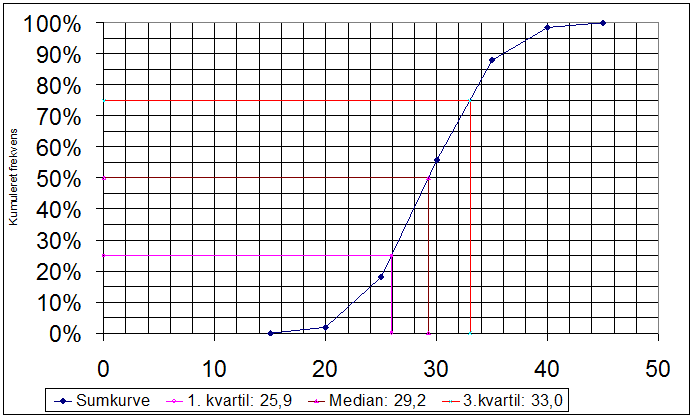
|
|
|
|
|
|
|
|
|
|
Medianen aflæses til 29,2 år
|
|
|
|
|
|
|
|
Medianen
fortæller , at halvdelen af de fødende kvinde er under 29,2 år
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opgave 2017
|
|
|
|
|
|
|
|
|
|
417000
er skovarealet målt i hektar i 1990
|
|
|
|
|
|
|
1,007
fortæller at skovarealet stiger med 0,7 % hvert år efter 1990
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opgave 2018
|
|
|
|
|
|
|
|
|
|
15
meter
høje rødgraner skal have en tæthed på: 168000*15^(-2)pr ha = 746,6…pr ha = 747
pr ha
|
747
|
pr hektar
|
|
|
Når
tætheden y er 3000 rødgran pr hektar må gælde:
|
|
|
|
|
|
3000
= 168000*x^(-2)
|
|
|
|
|
|
|
|
|
3000/168000
= x^(-2)
|
|
|
|
|
|
|
|
|
x
= (3000/168000)^(1/(-2))
|
|
|
|
|
|
|
|
x
= 7,5
|
|
|
|
|
|
|
|
|
|
Træhøjden skal være 7,5 meter
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Link til Indholdsfortegnelse
|
|
Regel
|
Formel
|
Eksempel
|
|
Helt
tal gange brøk
|
Det hele tal ganges ind i tælleren
|
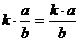
|
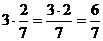
|
|
Brøk
gange brøk
|
Tæller gang tæller og nævner gang nævner
|
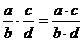
|
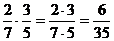
|
|
Brøk
divideret med
helt tal
|
Det hele tal ganges ind i nævneren
|
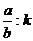 : :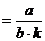
|
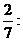 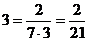
|
|
Helt tal divideret
med brøk
|
Man dividerer med en brøk ved at gange med den
omvendte
|
|
k :
|
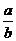 
|
|
|
|
Brøk
divideret med brøk
|
Man dividerer med en brøk ved at gange med den
omvendte
|
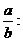  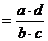
|
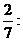 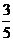 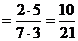
|
|
Forkorte
en brøk
|
Tæller og nævner divideres med samme tal
|
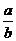 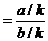
|
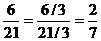
|
|
Forlænge
en brøk
|
Tæller og nævner ganges med samme tal
|
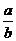 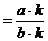
|
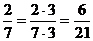
|
|
Brøk
plus brøk med
samme nævner
|
Tæller plus tæller og behold den fælles nævner
|
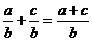
|
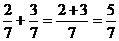
|
|
Brøk
minus brøk med
samme nævner
|
Tæller minus tæller og behold den fælles nævner
|
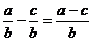
|
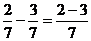 = = 
|
|
Find
fællesnævner
for 2 brøker
|
De to nævnere ganges med hinanden
|
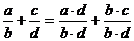
|
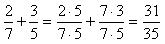
|