
Peter Sørensen
Matematik B
interaktivt for hf
(Gult
hæfte)
Version 8.1
Dette er en fortsættelse af matematik
interaktivt hf C-niveau.
Ved eksamen i matematik hf B-niveau
skal C-niveauet også kunnes.

©
PeterSoerensen.dk
Forord. 4
Lektion 19a
Genopfriskning af Matematik C: Brøk, ligning, eksponent, rod og parentes. 5
Brøk. 5
Ligninger 5
Eksponent og rod. 5
Parentes. 5
Lektion 19b
Genopfriskning af Matematik C: Procent , rente og indeks. 6
Procent og rente. 6
Indeks. 6
Lektion 19c
Genopfriskning af Matematik C: Sammenhæng mellem variable og funktioner. 7
Lektion 19d, modeller
og regression. 8
Absolut tilvækst 8
Relativ tilvækst 8
Matematisk modellering
og regression. 9
Regression og
CAS-værktøj 10
Excel regneark. 10
RegneRobot.dk. 10
CAS-lommeregneren TI-89
og Voyage 200. 11
Lektion 20a: Polynomier. 12
Parablens toppunkt 12
Lektion 20b: Polynomier. 14
Gør følgende 5 punkter 14
2) Læs. 14
Andengradsligningen. 14
Polynomier af n’te grad. 15
Polynomiets rødder
eller nulpunkter 15
Faktorisering af
polynomier 16
Lektion 21a,
Differentialregning. 17
Ikke alle grafpunkter
har en hældning. 18
Betydningen af ordet differentialkvotient 18
Differentiable
funktioner 19
Lektion 21b,
Differentialregning. 20
Bestemmelse af
differentialkvotient i praksis ved opgaveløsning. 20
Differentiation ved
hjælp af CAS-værktøj 20
Tangent 20
Ligningen for tangenten. 20
Linjeelement 21
Beregning af
differentialkvotienter 21
Differentiation af
udtryk. 22
Lektion 22, Anvendelse
af differentialregning. 23
Maksimum og minimum... 23
Monotoni 24
Lokalt maksimum... 24
Lokal minimum... 24
Monotoni-interval for
en funktion. 24
Voksende. 24
Aftagende. 24
Monotoniforhold. 25
Fortegnsvariation. 25
Optimering. 26
Lektion 23a
Stamfunktion og integral 27
Stamfunktion. 27
Integral (Ubestemt
integral) 27
Det bestemte integral 28
Lektion 23b
Stamfunktion og integral 29
Areal og integral 29
Regneregler for
bestemte integraler 30
Integraler /
stamfunktioner kan findes ved hjælp af CAS-værktøj 31
Lektion 24a
Vækstmodeller og funktionsteori, Ln og tallet e. 32
Tallet e. 32
Den naturlige
eksponentialfunktion. 32
Den naturlige logaritme. 32
Logaritmeregler 33
Eksponentielle funktioner 33
Differentialkvotient af
eksponentielle funktioner 33
Se også link: 33
Lektion 24b
Vækstmodeller og funktionsteori, Ln og tallet e. 34
Differentialkvotient af
Ln og stamfunktion til 1/x , ∫  dx. 34
dx. 34
Væksthastighed. 34
Lektion 25, Mere om
regression og CAS-værktøj 35
Lektion 26, Statistik og
sandsynlighed. 36
Normalfordeling. 36
Sandsynlighed. 38
Stikprøver 38
Lektion 27a Trigonometri 40
1) Repeter Lektion 9 og 17,
Geometri . 40
Se evt. links: Def. af Sin,
Cos og Tan Sinus, Cosinus og Tangens i regneark. 40
Idiotformlen. 40
Flere formler 40
Areal af trekant 41
Sinusrelationerne. 42
Lektion 27b Trigonometri 43
2) Læs. 43
Cosinusrelationen (Den
udvidede Pyhagoras) 43
Lektion 27c: Mere om
polynomier. 45
b’s geometriske betydning. 45
Parablens udseende. 45
Bevis for toppunktsformlen: 45
Bevis for løsningsformlen for
andengradsligningen. 47
Lektion 28, Eksamen og
repetition. 48
Eksempel på
undervisningsbeskrivelse. 48
Skriftlig eksamen. 48
Forberedelse af skriftlig
eksamen. 49
Pc. 49
Mundtlig eksamen. 50
Eksempel på
eksamens-spørgsmål 51
Forberedelse af mundtlig
eksamen. 52
Eksempler på dispositioner
til eksamensspørgsmål 52
Facitliste. 59
Supplement til formlerne i
blåt hæfte. 60
Forord
Dette hæfte er en del af et interaktivt
læresystem i matematik hf, og beregnet til at blive brugt på en pc med Explorer
koblet på Internettet (mahf.dk). Herved bliver det muligt at benytte diverse links til E-opgaver,
interaktive opgaver og til videoer. Sideløbende hermed kan det være praktisk at
benytte en papirudgave, som kan printes direkte fra mahf.dk.
På mahf.dk findes dette hefte både i HTML-format
med links og i et printvenligt PDF-format, hvor de fleste links er inaktive.
Videoerne bør ses i brudstykker på kun nogle
få minutter af gangen.
Besvarelser af
E-opgaver sendes automatisk via Internettet til læreren.
Med denne matematik-pakke følger endvidere et
elektronisk afleveringsark, RegneRobot med matematik-editor og CAS , hvor
elever/kursister kan besvare opgaver og også her automatisk få sendt
opgavebesvarelserne til læreren.
RegneRobot indeholder en række faciliteter,
der gør det lettere at besvare opgaver.
Indholdsfortegnelsen kan benyttes som links.
Uanset hvor man er i dokumentet, kan man komme
til indholdsfortegnelsen ved at taste Ctrl+Home , PageDown , PageDown.
Søgning på bestemte ord (svarende til
stikordsregister) foretages ved at taste Ctrl+f
Denne version, Matematik B interaktivt for
hf, version 8.1 er næsten magen til version 8, der adskiller sig en del fra de
tidligere versioner. En del lektioner er med mere forklaring, de store
lektioner er blevet opdelt til flere mindre lektioner og behandlingen af regneark
er blevet neddroslet. Behandlingen af TI-interactive er helt fjernet. Tidligere
versioner kan fås via www.lyngbydata.dk/skriv
Denne undervisningspakke er under stadig
udvikling. Forslag og eventuelle rettelser til denne pakke modtages med tak på lyngbydata.dk/rettelser
Matematik-pakken
kan bestilles via lyngbydata.dk/pakke
Gør følgende 3 punkter
1) Læs og genopfrisk matematik
C ved hjælp af nedenstående link.
Hvis du opdager, du mangler at lære noget
matematik fra C-niveau, så brug det grønne
og blå hæfte med links og videoer, især følgende
link: www.lyngbydata.dk/matematik
Se eventuelt link: Regler fra formelsamlingen i blåt hæfte
Genopfrisk brøkregning ved hjælp af dette link
til interaktive øve-opgaver: Brøkstykker
Hvis det kniber med de 4 regningsarter så benyt følgende link: Små opgaver i de 4
regningsarter
Se eventuelt link: Regler fra side 5 i grønt hæfte og fra
formelsamlingen i blåt hæfte
Genopfrisk ligninger ved hjælp af dette link:
Ligninger
Se eventuelt link: Regler fra lektion 3 og fra formelsamling
Genopfrisk eksponent og rod ved hjælp dette
link: Øvelse
Se eventuelt link: Regler fra formelsamlingen i blåt hæfte
Genopfrisk parentes ved hjælp af dette link: Parentes
2) Løs E-opgaver
Du afleverer elektronisk, når du klikker i Aflever
.
Link: E-opgaver 19a Genopfriskning broek og parentes
3) Løs opgaver fra 2006-opgavehæftet : 1.001 , 1.002 og 1.004
Benyt RegneRobot med link til opgavehæftet.
Klik i opgavenummeret og se en demo-video.
Også i RegneRobot afleveres elektronisk ved at klikke i Aflever .
Link til RegneRobot og opgavehæfte
Gør følgende 3 punkter
1) Læs og genopfrisk matematik
C ved hjælp af nedenstående link.
Se eventuelt link: Regler fra formelsamlingen i blåt hæfte
Genopfrisk procent og rentesregning ved hjælp
af dette link: Øvelse
Man udvælger et år, som
kaldes basisåret, og her sættes indeks til 100.
Indeks for de øvrige år
findes ved at fremskrive 100 med samme fremskrivningsfaktor, som de oprindelige
tal fremskrives med. Man kan således beregne indekstal ved først at beregne
disse fremskrivningsfaktorer.
Man kan også beregne
indekstal ved at udnytte proportionaliteten mellem de oprindelige tal og
indekstal. Proportionalitet er forklaret i Grønt hæfte, lektion 10, og ganske
kort i den følgende lektion 19c.
Hvis man kender indekstal
svarende til et basisår, kan indekstal svarende til et andet basisår beregnes.
Indeks er forklaret i
Grønt hæfte, lektion 8.
Se eventuelt: Regler fra formelsamlingen i blåt hæfte.
Løs følgende interaktive øve-opgave, link: indeks-opgave
2) Løs E-opgaver
Link: E-opgaver 19b Genopfrisk procent og indeks
3) Løs opgaver fra 2006-opgavehæftet: 3.006 og 3.012
Klik i
opgavenummeret og se en demo-video.
Link til RegneRobot og opgavehæfte
Gør følgende 4 punkter
1) Læs
Sammenhæng mellem variable og funktioner er udførligt
forklaret i lektion 10, 11, 13, 14 og 15. Her skal kort gentages de vigtigste
ting.
Hvis nedenstående er besværlig læsning, så
gå til lektion 10, 11, 13, 14 og 15.
En talstørrelse, der kan variere, fx
temperaturen i grader kaldes en variabel.
Hvis man måler temperaturen et bestemt sted en
bestemt dag, vil temperaturen normalt variere i løbet af dagen.
Vi siger, temperaturen afhænger af
tidspunktet eller, at temperaturen er en funktion af tiden.
Tidspunktet angives med et tal, der fx
angiver, hvor mange timer, der er gået siden midnat.
En sådan funktion kan vi give et navn fx f, og temperaturen til tiden x betegnes
f(x) og kaldes funktionsværdien af x .
Hvis funktionsværdien betegnes med y
fås y = f(x).
f(x) udtales ”f af x” .
Mængden af x-værdier, hvor f er
defineret kaldes definitionsmængden for f eller Df.
Mængden af funktionsværdier kaldes værdimængden
for f eller Vf.
Definitions- og værdimængden er ofte
intervaller, fx [0; ∞[, (tallene fra og med nul til uendelig).
Ofte er en funktion fastlagt ved en såkaldt
regneforskrift, fx: f(x) = 2x + 3, Dm = [0; ∞[
En funktion kan illustreres med en graf
i et koordinatsystem.
Grafen er de punkter, der har x som
x-værdi og f(x) som y-værdi
Hvis y = kx , hvor k
er et konstant tal, siger vi, y er ligefrem proportional
med x eller
blot proportional med x,og
k kaldes proportionalitetsfaktoren. Fx y = 10x
Hvis y = k · 1/x eller
x·y = k , hvor k er et konstant tal, siger vi, y
er omvendt proportional med x, og
k kaldes proportionalitetsfaktoren. Fx y = 10 · 1/x
eller x·y = 10.
En lineær funktion er en funktion, hvor
grafen er en linje eller en del af en linje.
En lineær funktion har en regneforskrift af
formen f(x) = ax + b , hvor a og b
er konstante tal.
10-talslogaritmen
til et tal er den eksponent man skal sætte på 10 for at få tallet.
En eksponentiel funktion er en funktion med en regneforskrift af formen f(x)=b·ax,
a>0 og b>0.
En potensfunktion er en funktion med en
regneforskrift af formen f(x)= b·xa, b>0 og x>0.
Se eventuelt: Regler fra formelsamlingen i blåt hæfte.
2) Løs interaktive øve-opgaver: proportionalitet Lineær funktion Eksp. funktion Potensfunktion
3) Løs E-opgaver E-opgaver 19c Genopfrisk variab.sammenh.& funktion
4) Løs opgaver fra 2006-opgavehæftet : 1.005, 1.013,
1.014 og 1.015
Link til RegneRobot og opgavehæfte
Lektion 19d, modeller og regression
1) Læs
Nogle
matematiske ord
|
Ord:
|
Forklaring:
|
Eksempler/
illustration:
|
|
faktor
|
En størrelse, der
skal ganges med.
|
5·8 Både 5 og 8
er faktorer.
|
|
produkt
|
Resultatet af et
gangestykke
|
5·8 = 40
40 er
produktet af 5 og 8
|
|
tæller
|
Den størrelse i en
brøk, der er over brøkstregen
|
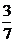 Brøkens tæller er 3. Brøkens tæller er 3.
|
|
nævner
|
Den størrelse i en
brøk, der er under brøkstregen
|
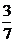 Brøkens nævner er 7. Brøkens nævner er 7.
|
|
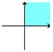
Første kvadrant
|
Den del af et
koordinatsystem hvor både x og y er positive
|
|
|
Andet kvadrant
|
Den del af et
koordinatsystem hvor x er nagativ og y er positiv
|
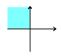
|
|
Tredje kvadrant
|
Den del af et
koordinatsystem hvor både x og y er negative
|
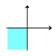
|
|
Fjerde kvadrant
|
Den del af et
koordinatsystem hvor x er positiv og y er negativ
|
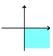
|
Symboler:
I det følgende bruges Dx , Dy , Ú og ó
Dx
er en forkortelse for x-tilvækst.
Dy
er en forkortelse for y-tilvækst.
Hvis man har en x-værdi, fx 5, og giver x en tilvækst på 2, så bliver den nye x-værdi 7,
og vi siger Dx = 2 . Nogfen gange siger vi, at den absolutte
tilvækst er 2.
Tilsvarende med andre variable. Når en
variabel fx y varierer fra en værdi
til en anden værdi, kaldes forskellen Dy den absolutte tilvækst.
Når en variabel fx y varierer
fra en værdi y0 til en anden værdi kalder vi
forskellen i forhold til startværdien y0 for den
relative tilvækst.
Den betegnes således: 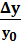 og
i procenter således:
og
i procenter således: 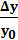 · 100 %
· 100 %
Ú
er nærmest en forkortelse af
ordet ”eller”.
Ú
betyder, at det til venstre for
Ú er sandt eller det til højre for Ú er sandt.
Fx
gælder følgende 3 udsagn:
(2+2
= 4) Ú (2+2 = 5) Det til venstre er sandt
(2+2
= 4) Ú (2+2 = 4) Det til højre er sandt
(2+2
= 4) Ú (3+2 = 5) Både det til venstre og det til
højre er sandt
ó er nærmest en forkortelse for ordet ”ensbetydende” og
kaldes ofte dobbeltpil.
ó betyder at
det som er før og efter ó er sandt for det eller
de samme x.
Fx
x=5 Ú x =-5 ó x²
= 25
x = 7 ó 2 x =14
I
sidste tilfælde er der kun ét x, som gør hver
ligning sand.
Nedenstående forklaring af regneark
forudsætter et forhåndskendskab til regneark. Se eventuelt lektion 6 og 12 i
grønt hæfte.
Mange fænomener kan med god tilnærmelse
beskrives ved en matematisk funktion.
Den matematiske funktion er en forenkling af
virkeligheden. Vi kalder den matematiske funktion en model af virkeligheden.
Fx kan en lineær funktion bruges som model for
befolkningsudviklingen i USA, mens befolkningsudviklingen i Indien bedre
beskrives ved en eksponentiel model.
Funktionen f(x) = 12x + 25 en model for taxa-kørsel, idet x er antal
km og f(x) er prisen, men i virkeligheden er prisen også afhængig af hvor mange
gange taxaen skal holde stille under vejs
bl.a. ved rødt lys. Den virkelige pris kan være ret besværlig at beskrive.
Derfor er det praktisk med modellen: f(x) = 12x + 25. Det kaldes en lineær
model.
Funktionen f(x) = 12x + 25 kan imidlertid også
være model for andre ting.
Lad os betragte et ur, der bliver stillet 25
sekunder forkert. Uret er 25 sekunder foran lige efter, det er stillet.
Derefter vinder uret ca 12 sekunder i døgnet nogen gange lidt mere og nogen
gange lidt mindre..
Urets fejlvisning kan med god tilnærmelse
beskrives ved modellen f(x) = 12x + 25, hvor x er antal døgn efter uret blev
stillet.
Det var et eksempel på, at vi kan bruge den
samme matematiske model til at beskrive 2 helt forskellige ting.
Hvis vi skal beregne, hvor meget uret er foran
efter 10 døgn bliver det således præcis den samme matematiske beregning som at
beregne prisen for 10 km med taxa.
Hvis man vil undersøge om en udvikling bedst
beskrives ved en lineær funktion, ved en eksponentiel funktion eller ved en
potensfunktion, kan man afsætte funktionsværdierne i mm-papir, i enkelt
logaritmisk papir og i dobbelt logaritmisk papir og vurdere, hvor punkterne
bedst flugter en linje.
Hvis man vil finde regneforskriften, kan man tegne linjen, den såkaldte tendenslinje, og beregne
regneforskriften ud fra 2 punkter, som aflæses på linjen. Det er imidlertid
meget lettere og bedre at bruge CAS-værktøj.
At finde den lineære funktion, som bedst
flugter nogle støttepunkter kaldes lineær regression.
Tilsvarende med eksponentiel regression
og potensregression.
Metoden i ovenstående kapitel med at tegne en
linje på et stykke papir er gammeldags.
Regression bør foretages med såkaldt
CAS-værktøj. Det er hurtigere, lettere og mere præcist.
Her vil blive gennemgået 4 slags CAS-værktøj: Excel
regneark, RegneRobot, TI89/Voyage 200 og TI-Nspire.
Du kan selv vælge hvilken slags CAS-værktøj, du vil lære at bruge.
I Grønt hæfte, lektion 12, er forklaret,
hvordan man automatisk kan få tegnet grafer i Excel regneark. Læs det.
I regneark Excel er det muligt at få tegnet tendesnlinjen
automatisk ved først at få tegnet en graf ud fra støttepunkterne og derefter
højreklikke med musen i grafen og vælge tendenslinje og funktionstype, fx ”eksponentiel”
. Det er endog muligt at få vist regneforskriften ved at vælge ”Vis ligning
i diagram”.
Hvis man ikke får valgt”Vis ligning i
diagram” samtidigt med at tendenslinjen tegnes, kan man højreklikke i
tendenslinjen og vælge ”Formater tendenslinje” og derefter vælge vælge ”Vis
ligning i diagram”.
Hvis man ønsker en logaritmisk skala på
y-aksen, skal man højreklikke i y-aksen og vælge ”Formater akse”.
Herefter kan man vælge fx logaritmisk skala.
Regression kan foretages ganske enkelt i
RegneRobot.
Klik i Guide og vælg ”Regression”.
Derefter popper et lille vindue op for neden.
Vælg fx: Lineær regression.
Udfyld med x-
og y-værdier.
Klik i ”Beregn”.
Sådan
ser vinduet ud efter, der er klikket i ”Beregn”.

Se eventuelt Vejledning til RegneRobot.
Her kan a og b findes på flere
måder.
Herunder vises én af disse måder:
Lommeregneren skal være i almindelig
calculator-tilstand.
Tast eventuelt 2ND ESC H Enter eller CALC
HOME .
Du starter med at cleare x mv.
ved at taste: F6, 1 og Enter.
Derefter gør du følgende:
Indtast en liste med x-værdier, fx: {0, 1, 2,
3}.
Indtast en liste med de tilsvarende y-værdier,
fx: {86, 300, 690, 1380}.
Vælg eksponentiel regression
Vælg ShowStat. Men Pas På ! Ved
eksponentiel regression på TI-89 og Voyage 200kaldes begyndelsesværdien ikke b, men a, og fremskrivningsfaktoren kaldes ikke a, men b.
Indtastningen kan være således:
|
{
|
0
|
,
|
1
|
,
|
2
|
,
|
3
|
}
|
STO>
|
L
|
1
|
Enter
|
|
{
|
86
|
,
|
300
|
,
|
690
|
,
|
1380
|
}
|
STO>
|
L
|
2
|
Enter
|
|
Math
|
6
|
3
|
2
|
L
|
1
|
,
|
L
|
2
|
Enter
|
|
|
|
|
Math
|
6
|
9
|
Enter
|
|
|
|
|
|
|
|
|
|
TI-Nspire
Hvis du er interesseret i TI-Nspire, så se
denne video; men bemærk at videoen også orienterer
om matematik, du endnu ikke har lært.
2)
Løs E-opgaver Link: E-opg. 19d regression
3)
Regn
fra 2006-opgavehæftet
: 2.001, 2.005,
2.007, 2.008
Link til RegneRobot og opgavehæfte
Gør følgende 3 punkter
1) Læs
Et andengradspolynomium er
en funktion med regneforskriften:
p(x) = ax² + bx + c , hvor am0.
Eks.
p(x) = 2x² - 12x + 10 er et andengradspolynomium
|
Hvis a >
0 ser grafen for et andengradspolynomium sådan
ud (en glad graf):
|
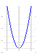
|
|
Hvis a <0 ser grafen for et andengradspolynomium sådan ud (en trist
graf):
|
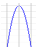
|
Disse
grafer kaldes parabler
Jo tættere a er på nul, jo mindre stejl er
parablen.
|
Det højeste eller
laveste punkt på en parabel kaldes toppunkt.
|

|
|
|
Idet vi indfører d = b² - 4ac gælder:
Koordinatsættet for
toppunktet er:
(
xo , yo ) = ( 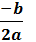 ,
, 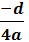 )
)
Denne formel vil blive bevist i lektion 27a
d kaldes diskriminanten.
Toppunktets y-værdi er
andengradspolynomiets mindsteværdi eller størsteværdi.
Hvis toppunktet er til venstre for y-aksen,
er 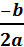 negativ og a og b har samme fortegn.
negativ og a og b har samme fortegn.
Hvis toppunktet/ er til højre for y-aksen, er 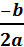 positiv og a og b har forskelligt fortegn.
positiv og a og b har forskelligt fortegn.
Hvis toppunktet ligger på y-aksen, er 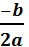 = 0 ó b = 0.
= 0 ó b = 0.
c er parablens skæring
med y-aksen. Det ses ved at indsætte x=0 i: y=ax² +bx+ c
a,b,c og d’s betydning for parablen
|
a
Grafens stejlhed
|
a<0:
Trist
graf
|
a=0:
Det
er ikke et 2.gradspolynomium
|
a>0:
Glad
graf
|
|
b
Grafens hældning ved 2.aksen
|
b<0:
Grafen
går nedad
ved 2.aksen
|
b=0:
Grafen
er vandret
ved 2.aksen
(Toppunkt
er på 2.aksen)
|
b>0:
Grafen
går opad
ved 2.aksen
|
|
c
Skæring med 2. aksen
|
c<0:
Grafen
skærer 2.aksens negative del
|
c=0:
Grafen
skærer 2.aksen i nul, koordinatsystemets begyndelsespunkt
|
c>0:
Grafen
skærer 2.aksens positive del
|
|
d
=b² - 4ac
|
d<0:
Grafen
skærer ikke
1. aksen
|
d=0:
Grafen
har ét punkt fælles med 1.aksen.
Dvs
toppunkt er på x-aksen
|
d>0:
Grafen
skærer 1. Aksen
to steder
|
1) Se
video, link: Andengradspolynomier
ved skriftlig eksamen
|
Hvis parablen skærer x-aksen
i to punkter kaldes de to steder nulpunkter eller rødder.
|
![[image]](start-3_14-filer/image020.jpg)
|
|
Hvis parablen har netop
ét punkt fælles med x-aksen kaldes det punkt/tal for nulpunkt,
rod eller dobbeltrod.
|
![[image]](start-3_14-filer/image021.jpg)
|
|
Hvis parablen ikke har
nogen punkter fælles med x-aksen, er der ingen rødder.
|
![[image]](start-3_14-filer/image022.jpg)
|
Vi vil nu se på hvordan man finder eventuelle rødder
for et andengradspolynomium.
Det handler om at løse en ligning, der kan
skrives på formen:
ax² + bx + c =
0 hvor am0
Der gælder:
Hvis d <0 bliver
der 0 løsninger. Parablen rører ikke x-aksen.
Hvis d =0 bliver der
1 løsning. Parablen rører x-aksen 1 sted.
Hvis d >0 bliver
der 2 løsninger. Parablen skærer x-aksen 2 steder.
|
Hvis d ≥ 0, kan ligningen løses ved hjælp af
formlen:
|
x = 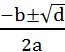
|
|
Dette vil blive bevist i lektion 27a
Eksempel
Grafen for p(x) = 2x² - 12x + 10
ser således ud
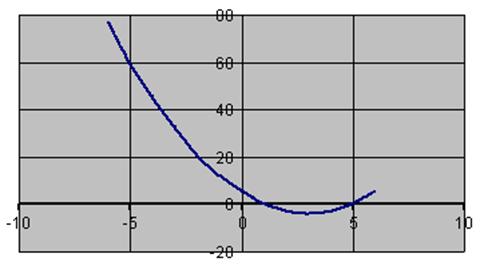
Rødderne kan aflæses hvor parablen skærer
x-aksen.
Løs ligningen 2x²
- 12x + 10 = 0 ved hjælp af CAS-værktøj eller følgende
link til en
skabelon i regneark: 2.gradspolynomiet.xls
Et polynomium er en
funktion med regneforskriften:
p(x) = anxn + an-1xn-1
+ …… + a2x² + a1x + a0 , hvor anm0 og n er et positivt helt
tal.
Polynomiets grad er n.
Eks.
2x3 –x2 – 7x + 17 er et
3.-gradspolynomium
Polynomiets rødder eller nulpunkter
er de eventuelle x-værdier, hvor p(x) = 0.
Lad os starte med at se et
eksempel på et andengradspolynomium: p(x )= 2x²-25x+30
Polynomiet kan omskrives til p(x)
= (x-3)·(5x-10), hvilket kan kontrolleres ved at gange parenteserne
sammen.
(Man
ganger 2 parenteser med inanden ved at gange vhert led i den nene med hvert led
i den anden.)
Det at omskrive 2x²-25x+30
til (x-3)·(5x-10) kaldes at faktorisere
polynomiet.
En størrelse, man ganger
med, kaldes en faktor, og (x-3)·(5x-10) består af 2 faktorer,
nemlig (x-3) og (5x-10) .
Hvis tælleren og nævneren
i en brøk er et polynomium, kan det være praktisk at faktorisere polynomiet.
Derved vil man nogle gange kunne forkorte brøken.
Altså til et produkt af to
faktorer.
Vi bemærker, at (x-3)·(5x-10)
= 0 hvis x=3. Dvs 3 er rod i polynomiet. (2 er i
øvrigt også rod.)
Generelt kan man
faktorisere er polynomium, hvis man kender en rod, og
polynomiet kan faktoriseres til (x minus roden) gange en størrelse fx (5x-10)
Det vil vi ikke bevise.
(5x-10) kan også faktoriseres, idet (5x-10) = 5·(x-2)
Alt ialt kan 2x²-25x+30
faktoriseres til 5·(x-3)·(x-2)
Altså til et produkt af 3
fakotrer, nemlig 5, (x-3) og (x-2)
Hvis man skal faktorisere
et polynomium er metoden aft finde polynomiets rødder.
Flere eksempler:
2x²-6x-8, -1 og 4 er rødder. Faktorisering: 2x²-6x-8
= 2(x+1)(x-4)
x² -2x+1, 1 er dobbeltrod. Faktorisering: x²
-2x+1 = (x-1)(x-1) = (x-1)²
Et n’te-gradspolynomium
kan højst have n rødder (nulpunkter).
Det vil vi ikke bevise.
Gør følgende 4 punkter
1) Se
videoer. Links: Diff 1 og Def
2) Læs
Grafen svarer til funktionen
f(x) = -2x² + 8x – 1,
Dm(f) = [0;5] , både x og f(x) er kroner i mio
Ved hjælp af grafen kan man aflæse at en rekaleminvestering på 2 mio kr vil
være optimal.
Vi skal nu se, hvordan man kan regne sig frem
til den mest optimale størrelse af reklameinvesteringen.
Der gælder, at funktionens mindsteværdi og
størsteværdi enten er ved et grafendepunkt eller hvor grafen er vandret, og det
er de steder, der skal checkes.
For at kunne beregne, hvornår grafen er
vandret, vil vi interessere os for grafens hældning.
Til enhver x-værdi i definitionsmængden vil ovenstående graf have en hældning,
der
betegnes f ’(x).
Vi har således en ny
funktion med samme definitionsmængde. Denne funktion betegnes f ’
og kaldes den afledede funktion, eller med et fint ord differentialkvotienten af f .
At finde
differentialkvotienten kaldes at differentiere.
Man kan også tale om den
afledede af en regneforskrift.
Fx betegnes den afledede af 8x-1 såedes: (8x-1)’
Vi vil ikke her præcist
definere ordet hældning/differentialkvotient, men lige nævne, at hældningen 0
betyder, at grafen er vandret. Ved Positiv hældning er funktionen voksende og
ved negativ hældning aftagende.
Hvis man skal finde en x-værdi,
hvor hældningen er 0, skal man således løse ligningen f ’(x) = 0
|
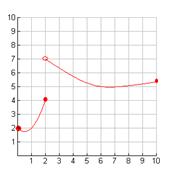
Til højre ses to grafer, der ikke overalt
har en hældning.
Den blå graf her ingen hældning i punkterne
(3, 2) og (7, 2.)
Den røde graf har ingen hældning i Grafpunktet
(2,4).
De to tilsvarende funktioner er ikke
differentiable i hele deres definitionsmængder.
|
![[image]](start-3_14-filer/image027.jpg)
|
|
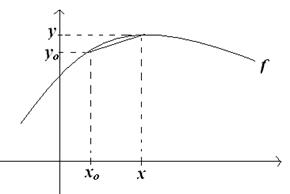 Betydningen af ordet differentialkvotient
Betydningen af ordet differentialkvotient
Her ser vi grafen for en funktion f, hvor
grafen har en hældning overalt..
Vi er interesseret i grafens hældning i punktet (xo , yo)
og beragter et punkt (x, y) tæt på ( xo , yo ).
Linjestykket fra punktet ( xo ,
yo ) til ( x , y ) er næsten sammenfaldende med grafen.
Et linjestykke, der forbinder 2 punkter på en
graf kaldes en sekant.
|
Jo tættere x er på x0 ,
jo bede vil sekanten flugte grafen,
Sekanten har hældningen: a = 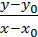 (Se lektion 11 i
Grønt hæfte)
(Se lektion 11 i
Grønt hæfte)
|
Lidt løst sagt defineres f´(x0)
eller grafens hældning i x0 således:
Hvis 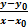 nærmer
sig en bestemt værdi, når x nærmer sig x0 , så er f´(x0)
lig denne værdi.
nærmer
sig en bestemt værdi, når x nærmer sig x0 , så er f´(x0)
lig denne værdi.
Denne værdi kaldes i
øvrigt grænseværdien for udtrykket når x går mod xo og
betegnes f´(xo).
Hvad det helt eksakt vil
sige at 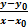 nærmer
sig en bestemt værdi, når x nærmer sig x0 , vil vi
ikke uddybe her.
nærmer
sig en bestemt værdi, når x nærmer sig x0 , vil vi
ikke uddybe her.
Det skrives således: 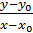 går mod f´(xo) når x går mod xo.
går mod f´(xo) når x går mod xo.
Det kan også skrives
sålees: 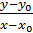 à f´(xo) når x à xo.
à f´(xo) når x à xo.
eller således: 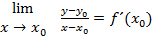
Ordet lim er i slægt med det engelske ord limit, der betyder grænse.
Ordet grænseværdi benyttes ikke blot ved
bestemmelse af grafers hældninger.
Generelt kan man tale om, at et udtryk, hvor
dets værdi afhænger af en variabel, kan have en grænseværdi, når denne variabel
nærmer sig et bestemt tal.
f ´ (xo) kaldes også differentialkvotienten
af f i xo eller blot differentialkvotienten i xo.
Ordet differentialkvotient
har noget at gøre med, at 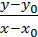 er en kvotient af differenser.
er en kvotient af differenser.
Kvotient betyder resultatet af en division, og differens
betyder resultatet af et minus-stykke.
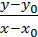 kaldes ofte differens-kvotienten.
kaldes ofte differens-kvotienten.
I gamle dage kaldte man
differenserne for differentialer, hvis differenserne var ekstremt små, og
derved opstod navnet differential-kvotient.
Vi benytter ofte
forkortelsen Df for f(x)
– f(x0) og Dx eller h for (x – x0)
Med disse forkortelser kan vi skrive:
|
f er
differentiabel i xo hvis
|
D x
|
har en grænseværdi for x ® xo
|
|
eller
|
|
|
|
f er
differentiabel i xo hvis
|
h
|
har en grænseværdi for h ® 0
|
Hvis en funktion f er differentiabel for
alle x, siger vi at funktionen er differentiabel,
og den funktion, der
til hvert xo knytter f´(xo) betegnes f ’.
f ’ kaldes differentialkvotienten af f eller den afledede af f.
Gør følgende 6 punkter
1) Se
videoer. Links: Tangent 3-trinsregel x² &
xn ax+b + reglen
2) Læs
Hvis
man kender regneforskriften for en funktion f, er det ofte muligt at
finde regneforskriften for den afledede funktion f ´ . Her benyttes
CAS-værktøj og forskellige regler. Vi vil senere bevise nogle af disse regler,
men først vil vi nøjes med at se nogle af reglerne:
|
( k )' = 0
|
Eksempel: f(x)=7 Grafen er vandret og f '(x)=0
|
|
(
k x )' = k
|
Eksempel: f(x)=3x Grafen har overalt hældningen 3 og f
'(x)=3
|
|
(xn)´ = n·xn-1 , n≠0
|
Eksempler: (x3)´ = 3·x3-1 = 3·x2 og
(x2)´ = 2·x2-1 = 2x
|
|
(k·f(x))' =
k·(f(x))' = k·f´(x)
|
Eksempel:
(2x3)´ = 2·3·x2 2 =
6x2
|
|
(k·xn) = k·n·xn-1 , n≠1
|
Eksempel:
(2x3)´ = 2·3·x2 =
6x2
|
|
(f(x)+g(x))´ = f ´(x) + g´(x).
|
Eksempel: (x³ + x²)' = 3x2 + 2x Plusreglen
|
|
(f(x)-g(x))´ = f ´(x) - g´(x).
|
Eksempel: (x³ - x²)' = 3x2 - 2x Minusreglen
|
Når man anvender
de 2 sidste regler kaldes det ledvis differentiation.
Når
der i et udtryk er 2 eller flere led, vil man typisk anvende ledvis
differentiation.
Der
er flere regler i formelsamlingen.
I RegneRobot differentieres ved at vælge "Guide
& CAS" og derefter "Differential- og integralregning".
Se eventuelt Vejledning til RegneRobot
På TI-89
og Voyage 200 kan man finde differentialkvotienten til en funktion,
fx f(x) = 3x² , ved at taste F3 og vælge d(
Derefter
skrives 3x^2,x) , så der kommer til at stå: d(3x^2,x)
(x til sidst betyder, at den uafhængige variable er x).
|
F6
|
Enter
|
Enter
|
F3
|
1
|
3
|
x
|
^
|
2
|
,
|
x
|
)
|
Enter
|
Der er mere om cas-væktøj i lektion 19, 23 og
25
En linje, der går gennem et grafpunkt og har
samme hældning som grafen i punktet, kaldes tangent til grafen.
Ligningen for tangenten gennem et grafpunkt (xo, yo)
er: (y – yo) = f ’ (xo)
(x – xo)
Hvis x ≠ xo ,
kan ligningen også skrives: 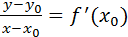
|
Til højre er tegnet funktionen f(x) = -2x² + 8x – 1 og en tangent.
Man kan se af tegningen, at hældningen er
-4.
Hældningen kan også beregnes:
f ’(x) = -4x + 8
f ’(3) = -4·3 + 8 = -12 + 8 = -4
Af tegningen ses, at tangentens røringspunkt er (3 , 5)
Tangentens ligning bliver: (y – 5) = –4(x
– 3)
|
![[image]](start-3_14-filer/image035.jpg)
|
|
Lad ( xo , yo ) være
et punkt på grafen.
De tre tal [xo , yo
, f '(xo) ] kaldes et
linjeelement for grafen.
Til højre illustreres linjeelementet: [-1,
3, 2]
og tangenten: y - 3 = 2(x - (-1)) ó y - 3 = 2(x + 1)
|
![[image]](start-3_14-filer/image036.jpg)
|
|
|
|
|
|
|
|
|
Hvis man kender en funktion og ønsker at finde
dens afledede er det ofte bekvemt at benytte den såkaldte tretrinsregel.
|
1. Opskriv 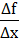 eller eller 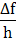 Husk h = Dx = (x-xo) og x= x0+h Husk h = Dx = (x-xo) og x= x0+h
2. Omskriv Df så der
kan forkortes med Dx eller h
3. Bestem
grænseværdien.
|
Eksempel 1 f(x) = ax +b
Da 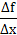 =
= 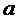 gælder også
gælder også 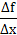 à
à 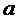 for x à xo
for x à xo
Altså: f’(xo)
= a. Da det gælder for ethvert xo
kan vi skrive f’(x) = a eller (ax+b)’ = a
Eksempel 2 f(x) = x²
Vi bemærker at x = xo + h , og vi får:
|
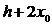
|
à
|
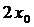
|
for x
|
à
|
xo
|
Altså: f’(xo)
= 2xo eller f’(x) = 2x eller (x²)’
= 2x
Vi vil bevise plus-reglen:
|
=
|
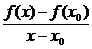
|
+
|
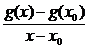
|
®
|
f '(x) + g '(x) for x ® x
|
Hvilket beviser (f+g)'(x)
= f '(x) + g'(x)
skives ved at tilføje en apostrof og ofte en
parentes, fx (x² + 2x)’ = 2x + 2.
Nogen gange sættes apostroffen anderledes, fx Log´x , som betyder
(Log x)’ .
|
Formlen
|
(xn)' = n·xn-1 , n≠0
|
vil
vi ikke bevise, men uddybe.
|
(x0)’
= (1)’ = (0x + 1)’ = 0. Det sidste fremgår af eksempel 1, hvor
a=0 og b=1. Altså (x0)’ = 0
(x1)’
= (x)’ = (1x + 0)’ = 1. Det sidste fremgår af eksempel 1, hvor
a=1 og b=0. Altså (x1)’ = 1 = x0
(x²)’
= (x·x)’ = 1·x + x·1 = 2x
(i
overensstemmelse med den tidligere beregning.)
(x3)’
= (x²·x)’ = 2x·x + x² ·1 = 3x²
(x4)’
= 4x3
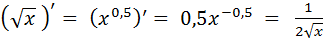 (Se
eventuelt lektion 3)
(Se
eventuelt lektion 3)
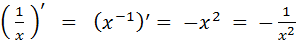 (Se eventuelt lektion 3)
(Se eventuelt lektion 3)
Gør følgende 4 punkter
1) Se video. Link: dif 2, anvendelse af differentialregning
2) Læs
Hvis en funktion er kontinuert på et lukket interval,
har den både et maksimum og et minimum.
Dette vil vi ikke bevise, men anskueliggøre
med nogle tegninger:

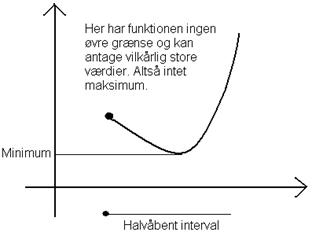
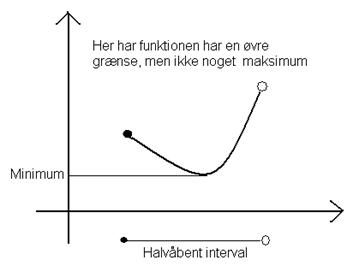
Bemærk:
Maksimum og minimum er y-værdier. De
tilsvarende x-værdier kaldes henholdsvis maksimumpunkt og minimumspunkt.
Hvis en funktion f er
differentiabel i et interval gælder:
|
f er voksende i intervallet
f er aftagende i intervallet
f er konstant i intervallet
|
hvis f
’(x) er positiv eller
punktvis nul.
hvis f
’(x) er negativ eller
punktvis nul.
hvis f
‘(x) = 0 overalt i
intervallet.
|
|
|
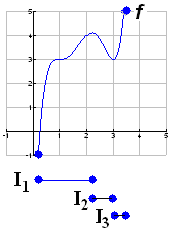
|
I
intervallet I1 er f ’(x) ≥ 0
og kun punktvis lig nul. (2 steder)
f er voksende i intervallet I1
I
intervallet I2 er f ’(x) ≤ 0 og kun
punktvis lig nul. (2 steder)
f er aftagende i intervallet I2.
I
intervallet I3 er f ’(x) ≥ 0
og kun punktvis lig nul. (1 sted)
f er voksende i intervallet I3
Bemærk:
I1 og I2 har 1 punkt fælles. Det gælder også
I2 og I3.
|
Lokalt maksimum
er en funktionsværdi, hvor grafpunktet ligger på en bølgetop eller på et vandret
stykke af grafen.
Det lokale maksimum er større end eller lig
y-værdien for de nærmeste punkter på grafen.
Lokal minimum
er en funktionsværdi, hvor grafpunktet ligger i en bølgedal eller på et vandret
stykke af grafen.
Det lokale minimum er mindre end eller lig
y-værdien for de nærmeste punkter på grafen.
Begge dele kaldes: Lokalt ekstremum. I
flertal: Lokale ekstrema.
Ved ekstremum er differentialkvotienten nul;
men differentialkvotienten kan også være nul andre steder.
Monotoni-interval for en funktion er et interval hvor
funktionen er monoton, dvs voksende, aftagende eller eventuelt konstant.
|
|
Om den afbillede
funktion gælder:
Voksende i ] - ∞; -3 ] og [ 1; ∞ [
Aftagende i [ -3; 1 ]
Lokalt
maksimum i -3 med y-værdi 34
Lokalt
minimum i 1 med y-værdi 2
Bemærk:
Begge tal -3 og 1
er med i både et voksende og i et aftagende interval.
|
|
Bemærk også:
Grafen er sammenhængende.
Derfor kan man ikke gå langs med grafen fra
et punkt under x-aksen til et punkt over x-aksen uden at
passere x-aksen. Et graf-punkt på x-aksen har y-værdien nul. En
funktion med en sammenhængende graf, kaldes kontinuert.
|
Monotoniforhold
At redegøre for monotoniforhold vil sige at oplyse
monotoniintervaller og anføre hvor voksende, hvor aftagende og hvor konstant.
Man
kan illustrere en fortegnsvariation over differentialkvotienten og se både
monotoniforhold og ekstrema.
Eks.
f(x) = x3 + 3x2
- 9x + 7
f’(x) = 3x2 + 6x - 9
For at finde ud af fortegnet for f ’
vil vi finde nulpunkter for f ’:
Dvs vi skal løse ligningen: 3x2 +
6x – 9 = 0
d = 36 – 4·3·(-9)
= 144
|
Rødder:
|
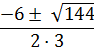
|
dvs. -3 og 1
|
Grafen for f ’ er ”glad” og derfor negativ mellem rødderne.

f er
voksende i ] -∞ ; -3 ] og [ 1 ; ∞ [
f er
aftagende i [-3
; 1 ]
Der hvor f skifter fra voksende til aftagende
har f lokalt maksimum,
altså ved x-værdien -3.
Selve maksimumsværdien er f(-3)
= 34
Tilsvarende bliver minimum = 2 der antages
for x =1
Ofte har man brug for at finde størsteværdi
eller mindsteværdi for en funktion.
Det at finde maksimum for en funktion kaldes
optimering.
Eks.
Vi betragter igen firmaet, som sælger en vare
og gerne vil optimere sin fortjeneste.
Se begyndelsen af foregående lektion.
x er
reklameinvesteringen i mio kr.
Den samlede fortjeneste ved salg af varen
afhænger af reklameinvesteringen.
f(x) er den samlede fortjeneste i mio kr ved salg af varen.
For den pågældende vare gælder:
f(x) = -2x² + 8x - 1 , Dm(f) = [0 ;
5]. Dvs der kan højst investeres 5 mio i reklamer
Det handler om af få maksimum fortjeneste.
f
’(x) = -4x + 8
f ’(x) = 0 ó
-4x + 8 = 0 ó x = 2
f
’(0) = 8 (positivt)
f
’(3) = -4 (negativt)
På grundlag heraf fås
Fortegnsvariation:
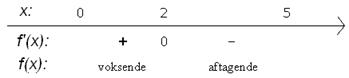
Resultat:
Der er maksimum fortjeneste ved en
reklameinvesering på 2
mio.
Maksimumfortjenesten er f(2) mio = 7 mio kr.
Vi kan også finde minimumfortjenesten ved at
vurdere f(0) og f(5)
f(0) = -1 mio
f(5) = -11 mio
Altså minimumsfortjenesten er -11 mio,
hvilket er et tab på 11 mio.
Bemærk, vi har stiltiende udnyttet at f´
er kontinuert. Derfor kunne vi konkludere, at når f´(0) er positiv, så
er f´(x) positv overalt til venstre for 2.
Tilsvarende kunnevi konkludere, at når f´(3)
er negativ,så er f´(x) negativ overalt til højre for 2.
Lektion 23a Stamfunktion og integral
Gør følgende 3 punkter
1) Læs
En funktion F kaldes stamfunktion til en funktion f hvis F’ = f.
Fx: F(x) = x² og f(x) = 2x
.
Der findes uendelig mange stamfunktioner til 2x
, bl.a. også (x²+7) idet (x²+7)’ = 2x
Der gælder, at alle stamfunktioner til 2x
er (x²+k) hvor k er et tal, der med et fint ord kaldes en
arbitrær konstant. Arbitrær betyder tilfældig eller vilkårlig.
Enhver af disse stamfunktioner kan betegnes
med den særlige skrivemåde: ∫2x dx , som udtales integralet af 2x
med hensyn til x. Nogen gange siger man det ubestemte integral.
Det er ubestemt hvilken
stamfunktion, der menes, når man skriver ∫2x
dx
Der gælder således ∫2x dx = x² + k , hvor k er en arbitrær konstant
At integrere en funktion vil sige at
finde stamfunktionerne.
Eksempler:
F(x) = x²
er en stamfunktion til f(x) = 2x , fordi (x²)’ =
2x
G(x) = x² +5
er en stamfunktion til g(x) = 2x , fordi (x² + 5)’
= 2x
Bemærk G(x) = F(x) + 5
Generelt kan man sige:
Hvis der til
en funktion f findes en stamfunktion F, så gælder:
1. G(x)=F(X)+k er også stamfunktion for f, idet k er et tilfældigt tal, kaldet en arbitrær
konstant.
2. Enhver stamfunktion til f kan skrives på formen G(x) =F(X)+k,
hvor k er et konstant tal.
Dvs. alle stamfunktioner til f
udgøres af dem, der kan skrives på formen G(x)=F(X) + k
Bevis:
1. G’(x)
= (F(x)+k )’ = f(x) + 0 = f(x). hvorfor G er
stamfunktion til f.
2. Vi betragter
stamfunktion til f : G.
(G(x) – F(x))’ = G’(x) – F’(x) = f(x) – f(x) = 0.
Grafen for (G(x) – F(x)) er derfor vandret overalt og (G(x) – F(x)) = et konstant tal k.
Altså G(x)=F(X)+k.
|
En stamfunktion til f kaldes
også det ubestemte integral til f og betegnes ∫ f(x) dx
Ofte siges blot integralet til f
Eksempler på integraler ses til højre, hvor k
er en arbitrær konstant og Ln er en særlig funktion, vi skal
lære om senere.
Løs interaktive øve-opgaver
Se regler for integration
|
|
f(x)
|
∫ f(x) dx
|
|
4x
|
2 x² + k
|
|
4x + 3
|
2 x² + 3 x + k
|
|
3
|
3 x + k
|
|
x²
|
⅓ x³ + k
|
|
3x²
|
x³ + k
|
|
6x²
|
2 x³ + k
|
|
x³
|
¼ x4 + k
|
|
5x³
|
5/4 x4
+
k
|
|
xⁿ (n ikke lig -1)
|
1/n+1 xn+1
+ k
|
|
x-1 (x>0)
|
Ln(x)
|
|
x-1 (x<0)
|
Ln(-x)
|
|
|
Lad F være en stamfunktion
til f.
Det bestemte integral af f fra a
til b defineres som F(b) – F(a) og betegnes 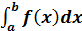
|
|
F(b) – F(a) kan kortfattet skrives således: 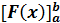
|
|
|
Altså:
Det bestemte integral af f fra a
til b =
|
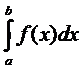
|
=
|
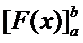
|
=
|
F(b) – F(a).
|
|
|
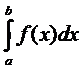
|
har samme værdi uanset hvilken stamfunktion
til f , man betragter.
|
|
|
|
|
|
|
|
|
Bevis
Hvis man betragter 2 forskellige
stamfunktioner til f ,
F1 og F2
, vil de kun adskille sig fra
hinanden ved en arbitrær konstant. Dvs F2 (x) - F1(
x) vil altid give den samme værdi uanset x.
Den værdi kan vi kalde k.
Det kan udtrykkes
således: F2
(x) - F1( x) = k ó F2 (x)
= F1( x) + k
Herefter ses det let at F2(b) – F2(a) har samme værdi som
F1(b) – F1(a),
idet F2(b) –
F2(a) = (F1(b) + k) – (F1(a) +
k) = F1(b)
– F1(a).
Bemærk
Det bestemte integral 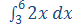 er et bestemt tal,
nemlig
er et bestemt tal,
nemlig 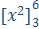 =
6²-3² = 36 - 9 = 27
=
6²-3² = 36 - 9 = 27
Det bestemte integral 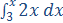 er
en bestemt funktion med regneforskrift:
er
en bestemt funktion med regneforskrift: 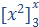 =
x²-3² = x²-9
=
x²-3² = x²-9
Vi skal i øvrigt snart
se, at 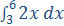 er
arealet af det område i koordinatsystemet, der ligger mellem intervallet [3; 6]
på x-aksen og grafen for 2x. Bemærk 2x>0 når x er i
intervallet [3; 6].
er
arealet af det område i koordinatsystemet, der ligger mellem intervallet [3; 6]
på x-aksen og grafen for 2x. Bemærk 2x>0 når x er i
intervallet [3; 6].
Gør følgende 5 punkter
1) Se
video. Link:
Stamfunktion og integral
2) Læs
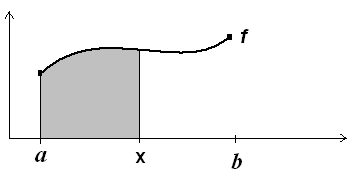
Ved integralregning kan man finde areal af
mange forskellige figurer. Vi vil nu betragte en funktion, som er positiv eller
eventuelt nul og kontinuert i et lukket interval [a; b].
x er et tal i intervallet.
|
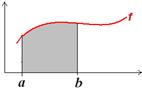
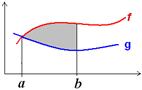
I tegningen til højre betragtes det
skraverede areal, der afgrænses af grafen, x-aksen og de lodrette
linjer gennem a og x.
Dette areal afhænger af, hvor i intervallet x placeres.
Arealet er således en funktion af x,
og kaldes arealfunktionen., Den vil vi betegne således: A
A(x) er således lig
det skraverede areal.
|
|
Der gælder:
A er en stamfunktion til f, og A er den
stamfunktion, hvor A(a) = 0.
Det vil vi ikke bevise, men anskueliggøre.
At A(a) = 0 virker temmelig indlysende.
At A er en stamfunktion til f
er også temmelig indlysende.
Det ses således:
|
Lad os betragte
|
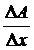
|
=
|
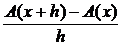
|
|
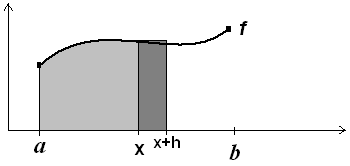
I tegningen her til højre vises situationen
ved en lille positiv h-værdi. Det virker troværdigt, at
tælleren er lig, eller næsten lig arealet af det mørkt markerede rektangel.
Dvs brøken er for små værdier af h
næsten lig rektanglets areal divideret med rektanglets grundlinje h og
det er rektanglets højde f(x).
|
|
Dermed har vi anskueliggjort, at
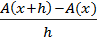 à f(x) for h à 0 (brøken nærmer sig f(x). når h nærmer sig nul)
à f(x) for h à 0 (brøken nærmer sig f(x). når h nærmer sig nul)
Altså, at A’(x) = f(x), som betyder, at A en
stamfunktion til f.
Bemærk
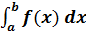 = A(b) - A(a) = A(b) – 0
= A(b) .
= A(b) - A(a) = A(b) – 0
= A(b) .
|
Dvs. hvis en graf for en funktion f ligger
over x-aksen på stykket fra a til b, kan man
beregne arealet af det område, der ligge mellem x-aksen og
grafen fra a til b således: 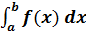
|
|
|
Arealet af området af fra a
til b mellem 2 grafer for funktionerne f og g,
hvor f(x)>g(x) kan beregnes således: 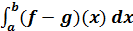
|
|
|
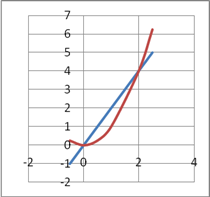
Eksempel:
f(x) = 2x , F(x) = x2
g(x)= x² , G(x) = 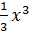
Arealet mellem de to grafer er
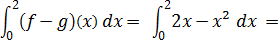
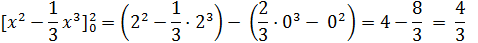
|
|
|
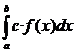
|
=
|
c ·
|
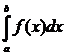
|
Den sidste regel kaldes Indskudsreglen
Eksempler:
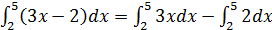 =
= 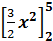
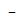
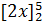 = ( 3/2
· 5² - 3/2 · 2² ) – (2·5 – 2·2) = 25½
= ( 3/2
· 5² - 3/2 · 2² ) – (2·5 – 2·2) = 25½
|
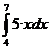
|
= 5 ·
|
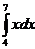
|
= 5 · 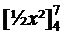 = 5 · ( ½ · 7² - ½ · 4² ) = 5 · 16½ = 82½ = 5 · ( ½ · 7² - ½ · 4² ) = 5 · 16½ = 82½
|
|
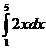
|
=
|
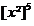
|
= 5² - 1² = 24
|
|
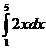
|
=
|
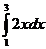
|
+
|
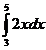
|
= 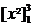 + + 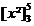 = (3² - 1²) + (5² - 3²)
= 5² - 1² = 24 = (3² - 1²) + (5² - 3²)
= 5² - 1² = 24
|
|
På TI89 findes f. eks.
|
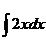
|
ved at taste:
|
|
F6
|
Enter
|
Enter
|
F3
|
2
|
2
|
x
|
,
|
x
|
)
|
Enter
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
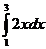
|
fås ved at taste:
|
|
F6
|
Enter
|
Enter
|
F3
|
2
|
2
|
x
|
,
|
x
|
,
|
1
|
,
|
3
|
)
|
Enter
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I RegneRobot skal du klikke i ”Guide & CAS” og vælge ”Differential-
og integralregning”. Se eventuelt Vejledning til RegneRobot.
Gør følgende 3 punkter
1) Læs
Fra Matematik C kender
vi:
Sammenhæng mellem variable
og funktion
Proportionalitet
Lineær funktion
Eksponerntiel Funktion
Logaitmefunktion (10-talslogaritmen)
Potensfunktion
Disse ting skal vi nu
arbejde videre med.
Vi skal møde et helt specielt tal, som spiller
en ganske stor rolle i matematikken.
Tallet kaldes e og er lig ca. 2,718.
Tallet kan ikke skrives som en endelig
decimalbrøk. Det er et irrationalt tal, altså et ikke rationalt tal, hvilket
vil sige, det ikke kan skrives som en brøk med helt tal for oven og helt tal
for neden.
Tallet er især interessant når det optræder i
den eksponentialfunktion, som har regneforskriften:
f(x) = ex
Denne funktion kaldes den naturlige
eksponentialfunktion og er karakteristisk ved at have sig selv som
differentialkvotient. Dvs f’(x)
= ex eller (ex)’ = ex
e kan
benyttes i RegneRobot. I nogle CAS-værktøjer skrives #e
Den naturlige logaritmefunktion betegnes Ln, og er bestemt
ved:
|
|
Den naturlige logaritme til et positivt
tal er den eksponent, man skal sætte på e for at få tallet.
|
|
DVS.
eLn(x) = x
.
Eksempler:
Ln(e3)
= 3
Ln(e7)
= 7
Ln(ex)
= x
Ln(ea)
= a
Ln(1) = 0 fordi e0 = 1
Ln(e) = 1 fordi e1 = e
Ln(a·b)
= Ln(a) + Ln(b)
Ln( ) = Ln(a) - Ln(b)
) = Ln(a) - Ln(b)
Ln(ax) = x· Ln(a)
Disse regler er magen
til reglerne for 10-talslogaritmen.
Nogen gange betegnes
den naturlige logaritme med lille l således: ln
Fx: ln(1) = 0
Vi vil nu omskrive b·ax, så e indgår.
Her får vi brug for en regel om eksponenter:
(ap)q
= ap·q , fx (53)2
= 5·5·5 · 5·5·5 = 53·2
Vi har tidligere set at x = eln(x), idet ln(x) er den eksponent, man skal putte på e for at få x.
Ved at skrive a i stedet for x fås: a = eln(a)
og ax = (eln(a))x = eln(a)·x
og b·ax = b·eln(a)·x
Derfor kan en eksponentiel funktion skrives på
følgende form: f(x) = b·eln(a)·x
Der gælder: (b·ax)’ =
ln(a) · b·ax (Det
vil vi ikke bevise)
Specielt gælder: (ax)’
= ln(a)·ax
Vi lægger mærke til, at differentialkvotienten
af en eksponentiel funktion er proportional med funktionsværdien.
Endvidere gælder: (b·enx)’ =
b·n·enx og (b·anx)’ =
ln(a) · n·b·anx
Det vil vi heller ikke bevise.
Eksempler:
(2·3x)’
= ln(3)·2·3x og (3x)’ = ln(3)·3x
Se også link: Regler for differentiation Bemærk især: (enx)’ =
nenx
På lommeregner Texas TI 89 og Voyage 200 kan (2·3x)’
findes ved at taste:
|
F3
|
1
|
2
|
*
|
3
|
^
|
x
|
,
|
x
|
)
|
Enter
|
Gør følgende 4 punkter
1) Se
video med stof fra både C- og
B-niveau. Link: Vaekstmodeller-funktionsteori
2) Læs
|
Der gælder: (ln(x) )’ =
|

|
, x > 0. (Det vil vi ikke
bevise.)
|
Tilsvarende: ∫  dx = ln(x)
+k , x
> 0. k er en abitrær konstant, dvs et vilkårligt tal .
dx = ln(x)
+k , x
> 0. k er en abitrær konstant, dvs et vilkårligt tal .
For x<0 : ∫  dx = ln(-x)
+k , x <
0.
(De 2 sidste formler vil vi heller ikke
bevise.)
dx = ln(-x)
+k , x <
0.
(De 2 sidste formler vil vi heller ikke
bevise.)
De 2 sidste formler kan under ét skrives ∫  dx = ln(|x|)
+k , x
dx = ln(|x|)
+k , x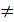 0 (x forskellig fra nul) ,
0 (x forskellig fra nul) ,
idet |x| betyder –x hvis x<0 og ellers x. Fx:
|-7|=7 og |7|=7.
(Bemærk,
vi bruger også den lodrette streg i geometri. Afstanden mellem fx punkterne A
og B betegnes: |AB| )
Se eventuelt Vejledning
til RegneRobot.
Se også formlerne
på sidste side: Naturlig
logaritme & eksponentialfunktion
Væksthastighed betyder det samme som
differentialkvotient.
Pakistans befolkning var i 2000 på 147 mio.
og er siden vokset med en væksthastighed på
1,71% pr. år.
Dvs: Væksthastigheden = 0,0171 · befolkningens
størrelse.
Væksthastigheden er således proportional med
befolkningens størrelse og proportionalitetsfaktoren er 0,0171.
Det kan skrives: f ’(x) = 0,0171· f(x),
hvor x er antal år efter år 2000 og f(x) er befolkningstallet, mens f ’(x)
er væksthastigheden.
Lektion 25, Mere om regression og CAS-værktøj
Gør følgende 3 punkter
1) Læs
I denne lektion skal vi repetere regression
og CAS-værktøj.
Se eventuelt lektion 19d.
Se eventuelt også Vejledning til
RegneRobot.
Gør følgende 5 punkter
1) Se lektion 16 om bl.a. sumkurve og histogram.
2) Se
video: Statistik og sandsynlighed
3) Læs
Når man skal beskrive et statistisk
talmateriale, kan man nogle gange sige, at observationerne er normalfordelt, og
allerede ved det er der sagt noget om, hvordan observationerne fordeler sig.
Der findes en lidt indviklet definition på
normalfordeling.
Her vil vi nøjes med at nævne nogle egenskaber
ved normalfordelinger:
Histogrammet ved en normalfordelinger er symmetrisk
omkring middeltallet, der således også er median.
Histogrammet ligner en klokke
Her ses et par klokkeformede histogrammer for
normalfordelinger med middelværdien 7 og ekstremt mange bitte små intervaller.
![[image]](start-3_14-filer/image117.png)
![[image]](start-3_14-filer/image118.png)
Man har lavet noget teknisk papir, som kaldes
normalfordelingspapir. Det er indrettet således, at netop normalfordelinger vil
få lineære sumkurver i dette papir. Sådant papir kan benyttes til at afgøre om
en fordeling er en normalfordeling. På næste side ses sumkurven for en
normalfordeling indtegnet i normalfordelingspapir. Medianen kan her aflæses til
4. Da det er en normalfordeling, er også middeltallet = 4
Tilsvarende kan nedre kvartil aflæses til 3,1
og øvre kvartil til 4,9

|
Opgave
Højden på danske soldater er normalfordelt.
5% af soldaterne har en højde på under 170 cm og 70 % af soldaterne har en
højde på under 185 cm. Udfyld skemaet til højre og indtegn sumkurven i
normalfordelingspapir. Aflæs kvartilsættet: (177, 182, 187)
Du kan eventuelt printe denne side og tegne
oven i.
|
|
Højde i cm
|
170
|
185
|
|
Kumuleret frekvens
|
|
|
|
Vi betragter et eksperiment med forskellige
udfald.
Fx kast med terning
Vi vil ikke nødvendigvis udføre eksperimentet,
men vi vil forestille os, at eksperimentet udføres mange gange.
Ved sandsynlighed for et bestemt udfald
forstås
den brøkdel af gange, man forventer udfaldet.
Eksempel
Hvis man kaster en
terning, er sandsynligheden for 6: 1/6 , og det er
den fordi, hvis man forestiller sig kastet gentaget mange gange, så forventer
vi, at frekvensen for 6 bliver 1/6 .
Opgave 0
Hvad er sandsynligheden for ikke at slå en
sekser?
Svar: 1 - 1/6 = 5/6
, da det at slå ”en sekser” eller ”ikke en sekser” er
udtømmende.
Opgave 1
Hvad er sandsynligheden for at slå en sekser
to gange i træk?
Svar: 1/6 ∙ 1/6 = 1/36
Opgave 2
Hvad er sandsynligheden for at slå 3 seksere i
træk?
Svar: (1/6)3
= 1/216
Opgave 3
Jeg kaster først en mønt og så en terning.
Hvad er sandsynligheden for, at det lykkes mig både at få krone og en sekser.
Svar: 1/2 ∙ 1/6 = 1/12
Vi bemærker, at sandsynligheden for nogle
bestemte udfald ved flere forskellige eksperimenter kan beregnes som produktet
af de enkelte sandsynligheder.
Man kan formode, at 10% af alle danskere vil
sige ja til fri heroin.
En sådan formodning kaldes en hypotese.
For at vurdere hypotesen vil vi foretage en
stikprøve. Vi vil spørge 20 tilfældige danskere, og er indstillet på at
forkaste hypotesen, hvis ingen af de 20 svarer ja.
Vi ved godt, at selv om hypotesen skulle være
sand, kan vi ikke udelukke, at der i vores stikprøve slet ikke er nogen, der
går ind for fri heroin, men vi antager, at sandsynligheden for det er meget
lille.
Lad os beregne den sandsynlighed. Altså sandsynligheden
for, at alle 20 svarer noget andet end ja, sunder forudsætning af at hypotesen
er sand.
For hver af de 20 tilfældige danskere er
sandsynligheden at få et ja: 10% = 0,10 og sandsynligheden for ikke at få ja: 90
% = 0,90.
Sandsynligheden for at alle 20 ikke svarer ja
er 0,9020 = 0,121… = 12%
Det er således 12 % sandsynligt, at vi kommer
til at forkaste en sand hypotese.
12 % er i den forbindelse temmelig meget og
spørgsmålet er, om det var en rimelig beslutning at forkaste hypotesen på
baggrund af en sådan stikprøve.
Vi vil nu spørge 100 tilfældige danskere, og
hvis ingen af dem siger ja, må vi vel kunne forkaste hypotesen.
Under forudsætning af at hypotesen er sand,
kan vi beregne sandsynligheden for, at vi alligevel forkaster hypotesen og får
0,90100 = 0,000026… = 0,003%.
Denne sandsynlighed er ekstrem lille, så hvis
resultatet af stikprøven bliver, at nul svarer ja, så tør vi godt forkaste
hypotesen. Det vil være næsten usandsynligt, at nul svarer ja ud af 100, hvis
10% af befolkningen skulle gå ind for fri heroin.
Måske ville det også være rimeligt at forkaste
hypotesen, hvis resultatet blev et enkelt ja.
Det at foretage en stikprøveundersøgelse af
100 personer er et eksempel på en såkaldt eksperimentserie bestående af 100 såkaldte
basiseksperimenter.
Hvert basiseksperiment består i at undersøge
om pågældende person vil svare ja.
Hvis hypotesen er rigtig, er sandsynligheden
for ja 10% , og det kalder vi basissandsynligheden, forkortet lille p.
Sandsynligheden for nej er 100% - p = 90%.
Udfaldet af stikprøven kaldes ofte χ
(χ er et græsk bogstav, der udtales noget i retning af ksi, men vi kan
bare sige store X)
Vi har beregnet sandsynligheden for (χ =0). Denne
sandsynlighed betegnes P(χ =0).
Sandsynligheden for et enkelt ja betegnes P(χ =1).
Sandsynligheden for netop 2 svar med JA
betegnes P(χ =2) osv.
Gør følgende 4 punkter
1) Repeter Lektion 9 og 17, Geometri
.
2) Læs
Nogle funktioner kaldes trigonometriske. Vi
skal arbejde med Sinus, Cosinus og Tangens.
Bemærk: Vores definition
af sinus og cosinus forudsætter ikke at vinklen skal være spids. Vinklen kan
være større end 360° og vinklen kan være negativ.
I definitionen af Sinus og Cosinus indgår en
trekant med grundlinjen på x-aksen. Det er en såkaldt standardtrekant.
Dvs. hypotenusen er 1.
Den til vinkel v hosliggende katete i
standardtrekanten er Cos v og den modstående er Sin v.
Ofte benyttes den forkortede skrivemåde Cos2 v i stedet for (Cos(v))2 og ligeledes Sin2v i stedet for (Sin(v))2 .
Ved hjælp af Pythagoras ses Cos2 v + Sin2
v = 12 = 1.
eller
Cos2 v + Sin2
v = 1
Denne formel kaldes populært idiotformlen.
|
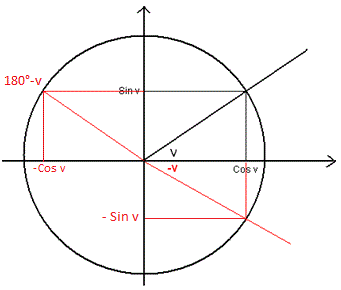
Ved at betragte tegningen til højre ses
|
Cos(-v) =
Cos v
|
Sin(-v) =
-Sin(v)
|
|
Cos (180°- v) = -
Cos(v)
|
Sin(180°- v) = Sin(v)
|
To vinkler, som tilsammen er 180º kaldes supplementvinkler
og den sidste formel kan udtrykkes:
Sinus
til supplementvinkler er lige store.
|
|
På C-niveau blev gennemgået, hvordan man kan
beregne vinkler og sider i retvinklede trekanter.
Her vil vi se hvordan, man gør hvis en
trekant ikke er retvinklet .
Først vil vi se på arrealet af en trekant.
Vi betragter en ΔABC , der ikke
nødvendigvis er retvinklet.
Vinkel C kan være spids, ret eller stump.
(Spids betyder under 90° og stump betyder over 90°)
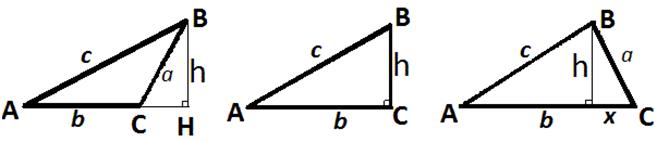
Bemærk: I figuren helt til venstre bliver vinkel BCH = 180°-
vinkel C
og derfor er Sin(vinkel BCH) = Sin(C)
Vi ved, at i enhver Δ ABC gælder: Arealet T = ½ højde · grundlinje
Altså: T = ½ h·b
Hvis man ikke kender h , men kender siderne a og b samt vinkel A, så kan man
beregne h.
Ved
at betragte tegningen længst til højre og den lille retvinklede trekant, der
afgrænses af h, a og x, ses at h kan
erstattes af a·Sin(C), idet Sin(C) = a/b
Det gælder også i den midterste tegning, da C her er 90° og Sin(C) derfor er 1.
Ved at betragte tegningen længst til venstre og den lille retvinklede trekant,
hvor
h er katete, ses at h også her kan erstattes af a·Sin(C),
fordi Sin(vinkel BCH) = Sin(C)
Således gælder i alle 3 situationer:
T = ½ h · b = ½ · a Sin C · b =
½ ab Sin C
Tilsvarende
fås
T = ½
ac Sin B og T
= ½ bc Sin A
Arealet = ½ · sinus til en vinkel ·
den ene hosliggende side · den anden hosliggende side
Endvidere gælder Herons formel: T= 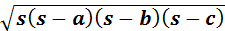 hvor
hvor 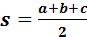
Den vil vi ikke bvise.
Vi skal nu se på hvordan man ud fra vinklerne
og en side i en trekant kan beregne de øvrige sider.
Regel:
I enhver trekant ABC gælder:

Bevis:
Vi betragter en vilkårlig ΔABC
Arealet T = ½ bc Sin A
= ½ ac Sin B = ½ ab Sin C
2T = bc Sin A = ac Sin B = ab Sin C
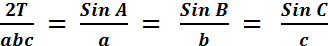
Hermed er reglen bevist.
Forholdet mellem sinus til
en vinkel og modstående side er ens for alle 3 vinkler
Sinusrelationerne kan
betragtes som ligninger, hvor den ubekendte er en trekantside, der kan findes
ved ligningsløsning.
Hvis man kender 2 sider og
en vinkel i en trekant, kan man også bruge sinusrelationerne og beregne sinus
til en af de andre vinkler i trekanten.
Men PAS PÅ!
Det betyder ikke altid, at man kan finde selve vinklen, idet 2 forskellige
vinkler kan have samme sinus. Fx: Sin 30° = 0,5 og Sin 120° = 0,5.
Mange gange kan man
imidlertid udelukke den ene af vinklerne, hvis den giver anledning til en
vinkelsum på over 180°.
|
5) Rapport
Skriv og aflever en rapport, hvor du
betragter en trekant ABC og ved hjælp af den gammel-kendte formel ” T = ½ hB ·
b ” beviser eller anskueliggører ” T = ½ ab Sin C ”
.
|
Gør følgende 4 punkter
1) Se
video: Trigonometri
Her skal vi se, hvordan man finder en side i
en trekant ud fra de andre sider og en vinkel..
Formel:
I enhver trekant ABC gælder: c² = a2
+ b2 – 2ab·Cos C .
Bevis:
Vi betragter en vilkårlig ΔABC
Der er 3 muligheder.
|
1) Vinkel C = 90°
|
|
2) Vinkel C < 90°
|
|
3) Vinkel C > 90°
|
|
1)
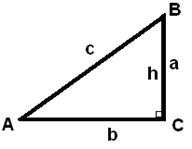
|
Højden fra B er sammenfaldende med siden
BC
Da vinkel C = 90°, er Cos(C) = 0
og formlens sidste led får værdien nul.
Formlen gælder således på grund af
Pythagoras sætning for retvinklede trekanter.
|
|
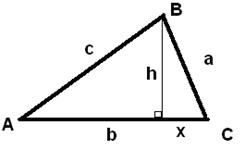
2) 
|
Højden fra B er inde i trekanten.
Ved Pythagoras fås:
c2
= (b - x)2 + h2
Men x og h
skal væk.
Derfor erstatter vi x
med a ·Cos C
og h
med
a
·Sin C.
c2
= (b – a·Cos C)2 + (a·Sin C)2
=
b2 + a2·Cos2C
– 2ba·Cos C + a2·Sin2C
a2
kan sættes uden for parentes
c2
= b2 + a2(Cos2 C + Sin2C) – 2ab·Cos2C
Ved hjælp af idiotformlen fås:
c2
= a2 + b2 – 2ab·Cos C
Hvilket skulle vises.
|
|
3)
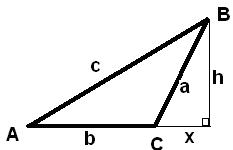
|
Højden
fra B er uden for trekanten.
Ved Pythagoras fås:
c2
= (b + x)2 + h2
Men x og h
skal væk.
Derfor erstatter vi x med a ·Cos(180°- C) = – a ·Cos C
og h med a ·Sin(180°– C) = a·Sin
C.
c2
= (b – a ·Cos C)2 + (a Sin C)2
=
b2 + a2·Cos2C
– 2ba·Cos C + a2·Sin2C
a2
kan sættes uden for parentes
c2
= b2 + a2(Cos2 C + Sin2C) – 2ab·Cos2C
Ved hjælp af idiotformlen fås:
c2
= a2 + b2 – 2ab·Cos C
Hvilket skulle vises.
|
Herved er formlen bevist i alle tilfælde.
|
Kvadratet på en side er lig summen af de to
andre siders kvadrater minus
2 · produktet af de to andre sider og cosinus til modstående vinkel.
|
Cosinusrelationen kan også bruges, hvis man
kender siderne i en trekant og vil finde en vinkel.
Så benyttes følgende omskrivning af
cosinusrelationen
Mens sinus til en trekantvinkel desværre ikke
altid entydigt bestemmer vinklen, så er det mere behageligt med cosinus. Når
man kender cosinus til en trekantvinkel, så er vinklen entydigt bestemt.
Gør følgende 6 punkter
1) Se
video, link:
Andengradspolynomier
I lektion 20 arbejdede vi med
polynomier. Her i denne lektion vil vi se nærmere på grafen for
andengradspolynomier, vi vil se b’s geometriske betydning, og vi vil bevise
toppunktsformlen og løsningsformlen for en andengradsligning.
Vi differentierer p(x)=ax²+bx+c, og får
p’(x) =2ax+b
Ved at sætte x=0, ser vi at b
er parablens hældning ved 2.aksen.
b’s
fortegn kan således direkte aflæses af parablen
|
Grafen for x² ser således ud:
(0,0) er toppunkt
|
![[image]](start-3_14-filer/image131.jpg)
|
|
Grafen for (x-3)² ser således ud:
(3,0) er toppunkt
|
![[image]](start-3_14-filer/image132.jpg)
|
|
Grafen for (x-3)²+2 ser således ud:
(3,2) er toppunkt
|
![[image]](start-3_14-filer/image133.jpg)
|
Generelt gælder at ethvert andengradspolynomie
kan skrives a(x-x0)²+y0
hvor (x0 , y0) er
toppunktet.
Det vil vi ikke bevise, men nøjes med
ovenstående anskueliggørelse.
( xo , yo ) = ( 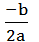 ,
,
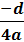 )
)
Vi vil nu betragte et vilkårligt andengradspolynomium ax² + bx + c.
Toppumnktet kan
karakteriseres ved at differentialkvotienten er nul.
Vi kan således finde x-værdien for
toppunktet ved at løse lignignen:
(ax² + bx + c)’ = 0
2ax+b = 0
x = 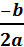
y-værdien for
toppunktet findes ved i polynomiet at erstatte x med 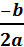 og vi får:
og vi får:
y = a·(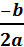 )2 + b ·
)2 + b · 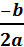 + c
+ c
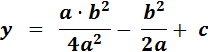
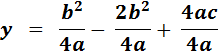
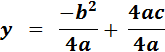
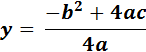
I lektion 20 indførte vi betegnelsen d for: b² - 4ac
- b² + 4ac bliver derfor lig -d og vi får
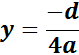
.
Koordinatsættet for
toppunktet bliver
således:
(
xo , yo ) = ( 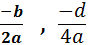 )
)
hvilket skulle bevises.
Det handler om at løse en ligning, der kan
skrives på formen:
ax² + bx + c = 0 hvor am0
Men det er meget lettere at løse ligningen,
når vi omskriver den ved hjælp af toppunktets koordinater til formen:
a(x - xo )² + yo = 0
a(x - xo )² = - yo
(x - xo )² = 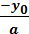
Venstresiden
kan ikke være negativ.
Hvis
højresiden er negativ, er der således ingen løsninger.
Vi
vil derfor vurdere højresiden og indsætter 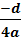 i stedet
for yo
. (Se toppunktsformlen)
i stedet
for yo
. (Se toppunktsformlen)
Højresiden bliver 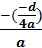 =
= 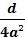
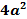 er
ikke negativ, så højresiden er kun negativ hvis d er negativ.
er
ikke negativ, så højresiden er kun negativ hvis d er negativ.
Der er således ingen
løsninger, hvis d er negativ.
Hvis d ≥
0 fås (x - xo )² = 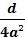
(x - xo
) = 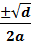
x - xo = 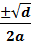
x = xo + 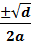
Vi indsætter 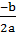 i stedet for xo og får x =
i stedet for xo og får x = 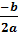
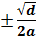
|
|
x = 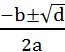
|
|
Vi har hermed bevist løsningsformlen. Hvis d=0 bliver der kun én løsning.
Gør følgende 4 punkter
1) Løs disse
E-opgaver, der meget vigtige ved forberedelsen af
mundtlig eksamen: 28a, 28b , 28c , 28d og 28e
2) Se eksamens-videoer
3) regn flere opgaver
fra 2006-opgavehæftet samt gamle
eksamensopgaver.
Link til RegneRobot og opgaverne
4) Læs
Pensum til eksamen er skrevet i en
undervisningsbeskrivelse. Både undervisningsbeskrivelsen og eksamensspørgsmål
offentliggøres i god tid før eksamen på kursets/skolens hjemmeside.
Eksempel på undervisningsbeskrivelse svarende til denne undervisningspakke:
Link: Undervisningsbeskrivelse
Der afholdes både en
skriftlig og en mundtlig eksamen
Mødetid er typisk kl 8:30 og selve prøven
starter kl 9:00.
Der bliver normalt udleveret papir før, selve
eksamen starter, og man kan under eksamen ved håndsoprækning bede om mere
papir.
Man kan bruge tiden, før selve eksamen starter
til at udfylde nogen stykker papir med navn, kursistnummer osv. .
Hvert stykke papir skal være udfyldt med
Navn,
Kursistnummer,
Holdnummer,
Sidenummer (nogen gange kaldet ark-nummer) og
antal sider/ark i alt (fx 3 af 5),
Prøve/Eksamen (Her skrives: HF),
Fag/niveau (her skrives: Mat. B).
Bemærk: antal sider/ark i alt er lig antal
stykker papir, som afleveres .
Der er ét sidenummer/arknummer til hvert
stykke papir.
Sidenummerering
er vigtig og fortæller censor i hvilken rækkefølge opgavebesvarelserne skal
læses og sikrer, at censor ser alle sider.
Hvis der også afleveres bilag på hvert sit
selvstændige stykke papir, så har hvert bilag sit eget sidenummer. Det kan være
hensigtsmæssigt at give bilagene de højeste sidenumre og tillige navngive hvert
bilag med et bogstav, fx bilag A, bilag B osv.
Husk at henvise til bilag fra de respektive
opgavebesvarelser, fx: ”Se bilag A”.
Klokken 9 udleveres to prøver. Den ene skal
løses uden hjælpemidler og afleveres kl 10:00. Der må ikke bruges pc før kl 10,
men gerne almindelige skriveredskaber, kuglepen, blyant, lineal osv.
Til den anden prøve må alle hjælpemidler
anvendes, også pc. Det er tilladt at gå på
Internettet i begrænset omfang. De hjemmesider, som skolen/kurset har benyttet
i undervisningen må du gerne benytte til skriftlig og mundtlig eksamen.
Det er således tilladt at
benytte RegneRobot til eksamen.
Man behøver ikke at lave kladde. Evt. kladde
og de trykte opgaver afleveres ikke og kan tages med hjem efter kl 13.
Nogen gange er de trykte opgaver suppleret med
et trykt bilag. Det er meningen, at man skal skrive eller tegne på bilaget (fx
aflæsninger og streger/markeringer). Bilag afleveres sammen med den øvrige
besvarelse.
Som ovenfor nævnt skal også bilag have
sidenummer mm.
Den skriftlige eksamen slutter normalt kl 13.
Kursister med problemer af forskellig art kan i god tid før eksamen søge om
forlænget tid.
Ca. en måned efter skriftlig eksamen, vil
kursisten kunne få sin skriftlige karakter.
Man forbereder sig ved at regne opgaver og ved
at regne nogle hele prøvesæt på 4 timer uden forstyrrelser.
Det anbefales at anvende pc. Ofte vil man
foretrække at løse nogle opgaver, eller dele af opgaver, på pc og resten
manuelt. Fx kan det være praktisk at lave en graf ved hjælp af en pc og
derefter med kuglepen tegne markeringer.
Opgavebesvarelser, der er lavet på pc, skal
printes på papir og kun papiret skal afleveres.
Det anbefales at printe siderne efterhånden.
Det vil også være ærgerligt, hvis man regner med at printe til sidst og ikke
når det. Desuden bliver besvarelserne på print ofte anderledes end forventet,
og der er brug for tid til at foretage ændringer.
Hvis pc’en bryder sammen kan man benytte de
sider, som allerede er printet, og resten skrives med håndkraft.
Ofte kan man benytte skolens printer via et
USB-stik, idet opgavebesvarelsern gemmes i PDF-format på USB-stikket, som så
flyttes over i Skolens printer. Hvis du benytter browseren Google Chrome, kan
du gemme i PDF-fomat fra RegneRobot ved at klikke i Print og skifte printer til
”Gem i PDF-format”
Kursisten
kommer ind i eksamenslokalet og får ved lodtrækning udleveret et stykke papir
med et eksamensspørgsmål.
Lodtrækningen vil typisk
foregå ved at kursisten vælger en seddel. På bagsiden af sedlen står et nummer,
der henviser til eksamensspørgsmålet.
Kursisten skal sikre sig
at spørgsmålet er forstået og kan spørge.
Kursisten får derefter
lejlighed til at forberede sig i sit eget lokale i ca 20 minutter. I særlige
tilfælde kan kursisten i god tid før eksamen søge om forlænget tid. Alle
hjælpemidler er tilladte, herunder egne og andres notater, dog er kommunikation
med omverden ikke tilladt.
Disse hjælpemidler må også
benyttes under selve fremlæggelsen af eksamensspørgsmålet, dog bør man ikke
kigge for meget i notaterne. Direkte oplæsning eller afskrift fra notater eller
lignende vil ikke tælle positivt ved bedømmelsen, altså give en dårligere
karakter.
Hvis man går i stå under
fremlæggelsen, kan man kigge i notaterne, men man bør holde mund mens man
kigger.
Mundtlig eksamen er
todelt.
Første del er kursistens
fremlæggelse (se
nedenstående dispositioner og videoer)
Anden del er samtale
Første del vil
typisk vare over halvdelen af tiden 12 à 20 min. Det er vigtigt, at kursisten i sin
fremlæggelse kommer ind på alle underpunkter i eksamensspørgsmålet. Derfor bør
man starte med disse underpunkter. Derefter fortsætter kursisten med andre
ting, der hører under hovedoverskriften. Hvis der er noget kursisten ikke kan,
fx et bevis, bør kursisten i sin fremlæggelse ikke bruge tid på det. Karakteren
bliver noget lavere, når kursisten springer noget over, men karakteren bliver
endnu lavere, hvis kursisten direkte demonstrerer sin manglende kunnen.
Anden del vil
typisk vare 5 à 10 min og tage udgangspunkt i kursistens fremlæggelse. Samtalen kan
ikke bevæge sig uden for hovedoverskriften.
Ca 5 minutter efter den mundtlige eksamen, vil
kursisten få sin mundtlige karakter.
1
Andngradspolynomiet
Definition af
andengradspolynomiet.
Gør rede for
andengradspolynomiets graf.
Bevis toppunktdformlen.
2.
Differentialregning
Gør rede for begrebet
differentialkvotient , gerne med udgangspunkt i din rapport.
Udled
differentialkvotienten for f(x) = x².
3.
Differentialregning
Gør rede for begrebet
differentialkvotient.
Gør rede for
regneregler for differentialkvotienter og bevis plus-reglen.
Inddrag gerne din
rapport.
4.
Differentialregning, eksponentiel funktion og den naturlige logaritmefunktion
Gør rede for den
naturlige eksponentialfunktion.
Gør rede for den
naturlige logaritmefunktion.
Gør rede for
differentiation af eksponentielle funktioner.
5.
Differentialregning og anvendelse af differentialregning
Gør rede for begrebet
differentialkvotient, gerne med udgangspunkt i din rapport.
Gør rede for
sammenhængen mellem monotoniforholdene for en
differentiabel funktion f og fortegnet for f ′ .
6. Vækstmodeller og
funktionsteori
Gør rede for funktionsbegrebet
og graf for en funktion.
Gør rede for lineær
funktion, eksponentiel funktion
og potensfunktion.
7. Stamfunktion og
integral
Gør rede for begrebet
stamfunktion og for sammenhængen mellem areal og stamfunktion.
8. Trigonometri
Gør rede for
definitionen af sinus og cosinus.
Bevis sinusrelationen
og formlen for arealet af en trekant.
Inddrag gerne din
rapport.
9. Trigonometri
Gør rede for
definitionen af sinus, cosinus og tangens.
Bevis
cosinusrelationen.
10. Statistik og sandsynlighed
Gør
kort rede for histogram og sumkurve ved grupperede observationer (lektion 16).
Gør rede for
sandsynlighedsbegrebet.
Omtal et eksempel på en
stikprøveundersøgelse.
Du skal desuden komme
ind på normalfordelingen.
Man forbereder sig
til mundtlig eksamen ved til hvert spørgsmål at udarbejde et foredrag og en
disposition.
Nogen af spørgsmålene
ligner hinanden og foredragene vil være næsten ens.
Man kan således nøjes
med at forberede ét foredrag til spørgsmål 2 og 3, og ét foredrag til
spørgsmål 4, 5 og 6, osv.
Der skal således
forberedes 7 foredrag.
Foredraget til
differentialregning bør indeholde alle de emner, der er i spørgsmål 1 og
spørgsmål 2 tilsammen og gerne lidt mere; men rækkefølgen er forskellig. Det er
som tidligere nævnt vigtigt, at man først taler om de emner, der er nævnt i det
spørgsmål man har trukket. Derefter kan man tale om de andre emner, der hører
under hovedoverskriften.
Det er en fordel at
forberede foredrag med så mange emner som muligt, så man har rigeligt at
fortælle om.
Sørg for at kunne
alle 7 foredrag lige godt.
Man bør på forhånd
have afprøvet alle 7 foredrag som en slags generalprøve. Det er en god idé at
være nogen stykker, der træner sammen ved en tavle og skiftes til at holde
foredrag for hinanden.
Du kan muligvis udbygge
disse dispositioner eller helt lave dine egne.
1
Andengradspolynomiet
Definition af
andengradspolynomiet.
Gør rede for
andengradspolynomiets graf.
Bevis toppunktdformlen.
Disposition:
Definition af
polynomier.
Parablen y=x² og forskydning af parablen mv. (Se video)
Toppunkt,
Rødder
Koefficienten til x²,
lille a, og a’s betydning for parablens udseende (glad eller trist).
Andengradsligningen
Udvikling af
løsningsformlen og betydningen af fortegnet for d.
Anvendelse af formlen
på et konkret eksempel fx 3x²+9x-12=0
.
Se link: lyngbydata.dk/video/videoer , Adgangskode: rewq
2.
Differentialregning
Gør rede for begrebet
differentialkvotient, gerne med
udgangspunkt i din rapport.
Udled
differentialkvotienten for f(x) = x².
Disposition
Definition af
differentialkvotient (lektion 21 og video)
Tangent til en graf
Udled
differentialkvotienten for f(x) = x².
Udled
differentialkvotienten for f(x) = ax +b
Sig at grafen for en
lineær funktion er sammenfaldende med tangenten i ethvert punkt
Differentier f(x)
= b (f’(x) = 0 i overensstemmelse med at
grafen for f er vandret)
Bevis plusreglen.
Du kan eventuelt
udbygge dispositionen ved at bevise minusreglen, du kan demonstrere hvordan man
differentierer med CAS-værktøj eller du kan gå videre med anvendelse af
differentialkvotient (lektion 22) eller du kan tale om differentiation af ex
og ax.
Se link: lyngbydata.dk/video/videoer
3.
Differentialregning
Gør rede for begrebet
differentialkvotient.
Gør rede for
regneregler for differentialkvotienter og bevis plus-reglen.
Inddrag gerne din
rapport.
Disposition
Definition af
differentialkvotient (lektion 21 og video)
Tangent til en graf
Bevis plusreglen.
Du kan evt. bevise
minusreglen
Udled
differentialkvotienten for f(x) = x².
Udled
differentialkvotienten for f(x) = ax +b
Sig at grafen for en
lineær funktion er sammenfaldende med tangenten i ethvert punkt
Differentier f(x)
= b (f’(x) = 0 i overensstemmelse med at grafen for f er
vandret)
Du kan eventuelt
udbygge dispositionen ved at bevise minusreglen, du kan demonstrere hvordan man
differentierer med CAS-værktøj eller du kan gå videre med anvendelse af
differentialregning (Lektion22) eller du kan tale om differentiation af ex
og ax.
Du kan også vælge at
tale om væksthastighed (lektion 24).
Se link: lyngbydata.dk/video/videoer
4.
Differentialregning, eksponentiel funktion og den naturlige logaritmefunktion
Gør rede for den
naturlige eksponentialfunktion.
Gør rede for den
naturlige logaritmefunktion.
Gør rede for
differentiation af eksponentielle funktioner.
Disposition
Definition af
differentialkvotient (lektion 21 og video)
Tangent til en graf
Tallet e
Den naturlige
eksponentialfunktion
Differentialkvotienten
af den naturlige eksponentialfunktion
Grafen for t= ex.
Definitionsmængde og værdimængde
Den naturlige
logaritme:
ln(x) defineret som det tal t, hvor et = x. Dvs. ln(x)=t ó et=x. Altså: eln(x) = x eller x =eln(x).
Bemærk at
x>0 fordi et>0
ax = eln(a) · x, (Det kan fx ses ved,
at tage den naturlige logaritme på begge sider)
(Det fremgår
også af, at x =eln(x) og dermed,
at a = eln(a)
.
Derved fås ax
= (eln(a))x = eln(a) · x . Se eventuelt lektion 3 og formelsamling)
(ax)’ = ln(a) · ax
(bax)’ =b · ln(a) · ax
(5 · 3x)’ = 5 · ln(3) · 3x
Differentialkvotient af ln(x) er 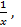 x
> 0
x
> 0
Du kan evt. udbygge og
vise hvordan, du differentierer med CAS-værktøj, eller du kan fortælle om
differentialregning med regneregler osv.
Du kan også vælge at tale om væksthastighed (lektion 24).
Se link: lyngbydata.dk/video/videoer
5.
Differentialregning og anvendelse af differentialregning
Gør rede for begrebet
differentialkvotient, gerne med udgangspunkt i din rapport.
Gør rede for
sammenhængen mellem monotoniforholdene for en
differentiabel funktion f og fortegnet for f ′ .
Disposition
Definition af
differentialkvotient (lektion 21 og video)
Tangent til en graf
Maksimum og minimum (lektion 22)
Monotoni og fortegn for f ’
Lokalt maksimum, lokalt minimum
Monotoni-interval
Fortegnsvariation, demonstreret på et
eksempel: f(x)
= x3 + 3x2 – 9x + 7 (lektion
22)
Eksempel, hvor
fortjeneste afhænger af reklameinvestering: -2x3+8x-1,
Dm=[0;5] (lektion 22). Du kan evt. også vælge at tale
om væksthastighed side 31, lektion 24.
Du kan evt. også
betragte et tog, der fjerner sig fra en station.
f(x) betegner er afstanden i meter efter x
sekunder,
f
’(x) er hastigheden
(meter/sekund)
Vi har ikke beskæftiget
os med at differentiere differentialkvotienten;
men den betegnes f ’’ og
kaldes den dobbelt afledede.
f
’’(x) kaldes accelerationen,
nemlig hastighedsændring pr sekund (meter/sekund²)
Se link: lyngbydata.dk/video/videoer
6.
Vækstmodeller og funktionsteori
Gør rede for
funktionsbegrebet og graf for en funktion
Gør rede for lineær
funktion, eksponentiel funktion og potensfunktion
Disposition
Variable (lektion 10,
video)
Funktion
Grafen for en funktion
Definitionsmængde og
værdimængde
Lineær funktion og
definition (lektion 11, video)
Eksponentiel funktion
og definition (lektion 14, video)
Potensfunktion og
definition (lektion 15, video)
Sig at disse funktioner
bruges som modeller af virkeligheden til at beskrive virkeligheden.
Differentialregning og
vækstmodeller. (Lektion 24)
Tallet e
Den naturlige
eksponentialfunktion
Differentialkvotienten
af den naturlige eksponentialfunktion
Grafen for t= ex.
Definitionsmængde og værdimængde
Den naturlige
logaritme:
ln(x) defineret som det tal t, hvor et = x. Dvs. eln(x)=x eller eln(a)=a
ax = eln(a) · x, (Det fremgår af, at
a = eln(a) .
Derved fås ax
= (eln(a))x = eln(a) · x . Se eventuelt lektion 3 og formelsamling)
(ax)’ = ln(a) · ax
(bax)’ =b · ln(a) · ax
(5 · 3x)’ = 5 · ln(3) · 3x
Differentialkvotient af ln(x) er 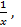 x
> 0
x
> 0
Du kan evt. udbygge og
vise hvordan, du differentierer med CAS-værktøj eller du kan fortælle om
differentialregning med regneregler osv.
Du kan også vælge tale
om væksthastighed (lektion 24).
Se link: lyngbydata.dk/video/videoer
7.
Stamfunktion og integral
Gør rede for begrebet
stamfunktion og for sammenhængen mellem areal og stamfunktion.
Definition af stamfunktion (lektion 23)
Eksempel: Stamfunktion til 2x: x2 + k , hvor k er en arbitrær konstant, dvs vilkårlig konstant.
Areal og integral (lektion 23)
Tegn en tegning som den første af tegningerne
i lektion 23.
Indfør A(x) som det markerede areal
Bemærk A(a) = 0
Udbyg din tegning til at være som den sidste
af tegningerne i lektion 23
Gør rede for at differentialkvotienten af A(x)
er lig f(x)
Konkluder: A(x) er den stamfunktion til
f, hvor funktionsværdien af a er 0
Areal af et område mellem to grafer
Det bestemte integral 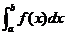
Regneregler for bestemte integraler og
eksempler
Eventuelt demonstration af anvendelse af
CAS-værktøj.
Se link: lyngbydata.dk/video/videoer
8.
Trigonometri
Gør rede for
definitionen af sinus og cosinus.
Bevis sinusrelationen
og formlen for arealet af en trekant.
Inddrag gerne din
rapport.
Disposition
Definition af Sinus og
Cosinus (lektion 27, video)
Areal &
Sinusrelationerne: (lektion 27, video)
Tegn 3 trekanter, hvor
vinkle C er henholdsvis spids, ret og stump. (lektion 27, video)
hA= a·Sin C, også når C er stump fordi
Sinus til nabovinkler er lige store.
Areal af trekant T =
½·ab·sin C (lektion 27, video)
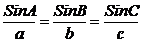
Eksempel:
a=2, b=4, Ð B = 30°. Sin A = 2·Sin30°/4 = 0,25. Ð A=14,5° eller (ÐA=165,5° Forkastet)
(Den sidste løsning
blev forkastet fordi ÐA+ÐB skal være mindre end 180°)
Cosinusrelationerne:
(lektion27, video)
Tegn de 2 situationer
Brug Pythagoras
Til venstre: x skal
trækkes fra b og x = a · Cos C og h = a· Sin C
Til Højre : x skal
lægges til b og x = a · Cos(180°-C) = - a · Cos C og h = a · Sin(180°-C)
= a · Cos C
a² sættes uden for
parentes og (Cos²C + Sin²C) = 1
Vi får c² = a² + b²
- 2a b · Cos A
Eksempel: Samme D, c2=22+42
– 2 · 2· 4 · Cos 135,5° = 34,66.. c=5,9
Se link: lyngbydata.dk/video/videoer
9.
Trigonometri
Gør rede for
definitionen af sinus, cosinus og tangens.
Bevis
cosinusrelationen.
Disposition
Definition af Sinus og
Cosinus (side 36, lektion 27, video)
Cosinusrelationerne:
(Side 42, lektion27, video)
Tegn de 2 situationer
Brug Pythagoras
Til venstre: x skal
trækkes fra b og x = a · Cos C og h = a· Sin C
Til Højre : x skal
lægges til b og x = a · Cos(180°-C) = - a · Cos C og h = a · Sin(180°-C)
= a · Cos C
a² sættes uden for
parentes og (Cos²C + Sin²C) = 1
Vi får c² = a² + b²
- 2a b · Cos A
Eksempel: Samme D, c2=22+42
– 2 · 2· 4 · Cos 135,5° = 34,66.. c=5,9
Areal &
Sinusrelationerne: (Side40,
lektion 27, video)
Tegn 3 trekanter som på
side 40, hvor vinkle C er henholdsvis spids, ret og stump.
hA= a·Sin C, også når C er stump fordi
Sinus til nabovinkler er lige store.
Areal af trekant T =
½·ab·sin C (side 40, lektion 27, video)
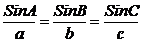
Eksempel:
a=2, b=4, Ð B = 30°. Sin A = 2·Sin30°/4 = 0,25. Ð A=14,5° eller (ÐA=165,5° Forkastet)
(Den sidste løsning
blev forkastet fordi ÐA+ÐB skal være mindre end 180°)
Se link: lyngbydata.dk/video/videoer
10.
Statistik og sandsynlighed
Gør kort rede for
histogram og sumkurve ved grupperede observationer (lektion 16).
Gør rede for
sandsynlighedsbegrebet. (lektion 26)
Omtal et eksempel på en
stikprøveundersøgelse.
Du skal desuden komme
ind på normalfordelingen.
Disposition
Betragt følgende observationssæt over højden
på danske soldater ved en bestemt kasserne
|
Højde i cm
|
160 à 170
|
170 à 180
|
180 à 190
|
190 à 200
|
|
Frekvens
|
5 %
|
38 %
|
52 %
|
5 %
|
|
Kumuleret frekvens
|
5 %
|
43 %
|
95 %
|
100 %
|
Vis hvordan du tegner histogram og sumkurve i
sædvanligt koordinatsystem (lektion 16)
Sig, at observationerne kan være normalfordelte.
(lektion 26)
Sig, at ved en normalfordeling er histogrammet
klokkeformet.
Sig, at der findes normalfordelingspapir.
Tegn sumkurven i normalfordelingspapir og
konkluder, at der er tale om en normalfordeling
Sandsynlighed, dvs den frekvens, man forventer
et bestemt udfald ved mange gentagelser. Sandsynlighed for 3 seksere i træk ved
kast med terning: 1/6 · 1/6 · 1/6
= (1/6)3 (Der ganges).
Hypotese: 10 % af alle danskere vil sige ja
til fri heroin.
Stikprøve på 20.
Hvis hypotesen er sand fås:
Sandsynlighed for at stikprøven giver et
udfald med ingen ja: 0,9020 = 0,121… = 12 %.
Dette udfald kan således let forekomme, og man
vil næppe forkaste hypotesen på baggrund af stikprøven.
Sandsynlighed for, at en stikprøve på 100
giver et udfald med ingen ja. 0,90100 = 0,003 %
Hvis hypotesen er sand, så er stikprøvens
udfald næsten umuligt. Vi vælger at forkaste hypotesen.
X betegner
stikprøvens udfald
P(X=0) betegner sandsynligheden for, at
udfaldet = 0.
Se link: lyngbydata.dk/video/videoer
Hermed link til
facitliste.
Link: Facitliste
til Eksamensopgaver
Supplement
til formlerne i blåt hæfte Andengradspolynomiet
|
p(x) =ax2 + bx + c
|
|
Diskriminanten
|
d = b²-4ac
|
|
Toppunkt: (xo , yo)
=
|
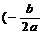 , , 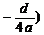
|
|
|
d < 0, c > 0, glad graf: a >
0
xo>o: b har fortegn modsat a
|
|
|
d > 0, c > 0, trist graf: a
< 0
xo<0: b har samme
fortegn som a
|
|
c er
skæring med y-aksen
b er hældning ved y-aksen
|
|
|
Rødder / nulpunkter
|
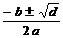
|
|
|
|
|
Differentialregning
|
( f
+ g )'(x) =
|
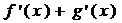
|
|
( f
– g )'(x) =
|
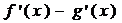
|
|
(k·f(x))' =
|
|
k·(f(x))'=k·f´(x)
|
fx: (5x³)´=15x²
|
|
|
(k·x)'
=
|
|
|
n ≠ 0: (xn)' =
|
|
|
n ≠ 0: (k xn)' =
|
|
|
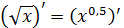
|
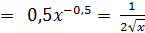
|
|
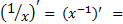
|
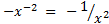
|
|
(x2
- 3x + 1/x)'
=
|
2x - 3 - x -2
|
|
Ligning for linje
gennem (xo , yo ) med hældning a
|
y - yo = a(x – xo)
|
|
|
Ligning for tangent
gennem (xo , yo )
|
y - yo = f '(xo)(x – xo)
|
|
|
Tangent til f(x)=x²
gennem (3,9)
|
f '(x)=2x og
f '(3)=6
Ligning: y - 9 = 6(x- 3)
|
|
|
|
|
|
|
|
Integral / stamfunktion
|
f(x)
|
∫ f(x) dx
|
|
4x
|
2
x² + k
|
|
4x
+ 3
|
2
x² + 3 x + k
|
|
3
|
3
x + k
|
|
6x²
|
2
x³ + k
|
|
x³
|
¼
x4 + k
|
|
5x³
|
5/4 x4 +
k
|
|
xⁿ
, n ≠ -1
|
1/n+1 xn+1
+ k
|
|
x-1
= 1/x , x>0
|
Ln(x)
+ k
|
|
ex
|
ex + k
|
|
bax
|
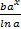 + k + k
|
|
Ln & ex
|
Ln(a·b)
=
|
Ln(a) + Ln(b)
|
|
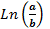 = =
|
Ln(a) - Ln(b)
|
|
Ln(ax) =
|
x· Ln(a)
|
|
eLn(a) =
|
a
|
|
eLn(a)· x =
|
ax
|
|
b·Ln(a)·eLn(a)· x =
|
b·Ln(a)·ax
|
|
(ax)’ =
|
Ln(a)·ax
|
|
(ex)’ =
|
ex
|
|
(k
enx)’ =
|
k·n·enx
|
|
Ln’x =
|
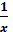 ,
x > 0 ,
x > 0
|
|
For x>0: ∫1/x dx =
|
ln(x) +k
|
|
For x<0: ∫1/x dx =
|
ln(-x) +k
|
Trigonometri
|
Cos2 C + Sin2C
=
|
1
|
|
Cos(-v)
=
|
Cos v
|
|
Sin
(180-v) =
|
Sin (v)
|
|
Radiantallet
=
|
Gradtallet · π/180
|
|
Gradtallet
=
|
Radiantallet · 180/π
|
|
Sin(π-x)
=
|
Sin(x)
|
|
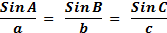
|
|
|
Sin A = a · 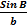
|
a = Sin A · 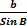
|
|
|
Areal: T
= ½ aha
= ½ ab Sin C
|
|
|
Herons formel: T=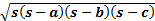
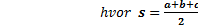
|
|
|
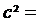
|
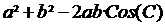
|
|
|
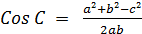
|
|
|
|
|
|
|
|
|